ie-Physics

Experiment I-2

Aristotle (384-322 B.C.) suggested that heavier objects fall faster than lighter ones towards the center of the cosmos, the earth.  Nearly 20 centuries later, Galileo Galilei (b1564, d1642 A.D. ←portrait left) believed that Aristotle badly misunderstood the behavior of the cosmos.  Galileo believed that the earth moved around the sun as suggested by Copernicus.  But this idea was criticized for lack of evidence and because it was inconsistent with Aristotle's causes of motions.  Late in life Galileo suggested that Aristotle's description of falling objects was also flawed, and furthermore, those flaws could be experimentally confirmed.

Galileo suggested that free from significant resistance, all objects fall the same.  They start from rest and accelerate constantly as they fall.  Galileo proposed that objects very different in weight would keep pace, even when dropped from great height such as from the bell tower at the cathedral of Pisa.

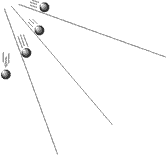
While Galileo might be right, he had no technology to actually measure the acceleration of a rapidly falling object.  So he reasoned that an inclined plane would dilute the fall of a ball, but not change the nature of the steady acceleration.

Galileo was able to mathematically show that if the acceleration is steady, the the distance fallen will be proportional to the square of the time of fall:  d = 1/2 at², where a is the acceleration constant.

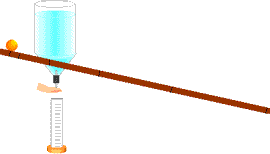
Galileo used a water clock to measure time.  If a large container of water is maintained at the same fill level, the amount of water allowed to flow out will be proportional to the time of flow.  The amount of water draining out is a direct measure of the time.  (i.e., twice as much water means twice the time elapsed.)

By using experimental evidence to overthrow ideas believed true for 2000 years, Galileo did much to start a new science that developed the most successful procedures known to human beings for learning about the universe.  For that reason (and many more), this is an experiment important to repeat and to understand.

Experiment

1. Measure distances down from the starting position on the ramp that are in relationships to perfect squares:  one arbitrary distance, 4 times that distance, 9 times the distance, 16 times, etc.  The ramp needs to be as straight and uniform as possible.  If the angle of the ramp is too shallow, imperfections in the ramp are more likely to cause errors in your measurements.  If the angle of the ramp is too steep, errors in timing will become more significant.
2. Repeatedly time the ball rolling down each distance using a water clock like Galileo used (or a stop watch).  Galileo said the times should be in the ratios of 1 : 2 : 3 : 4 : etc.  The distances transversed should be proportional to the squares of the water released (the elapsed times).
3. If Galileo is correct, a graph of the squares of the amounts of water verse distances should be a straight line from the origin.

Record your observations recorded in your journal.  If you need course credit, use the information in your journal to construct a formal report.

Frames of Reference & Galilean Relativity

Several principles of relativity were assumed by Galileo:  The laws of nature must be the same regardless of the person measuring them.  And any law of nature should be the same at all times.  In addition, motion observed by one person should be equivalent to what is observed by another.  Galileo first described this principle in 1632 in his Dialogue Concerning the Two Chief World Systems using the example of a ship traveling at constant speed, without rocking, on a smooth sea; any observer doing experiments below the deck would not be able to tell whether the ship was moving or stationary.

• Consider an event occurring nearly in from of an observer.  A second observer standing two meters to the left of the first observer would see the event displaced two meters to the right of what is observed by the first observer.  Each observer using their own frame of reference would not measure the object at the same location.  An object measured to be located at a distance of x to the right of in front of the first observer would be measured at a distance of x + 2 m to the right of the second observer.
  
  
• Consider an event observed by two people moving with respect to each other.  For example one might be riding on a vehicle moving at constant speed while the other may be stationary nearby (as in the videos below).  A ball dropped straight down by the rider , will seem to move forward in a parabolic path to the other.  And in a symmetrical experiment, a ball dropped straight down by the stationary observer would seem to fall backward in a parabolic path to the rider.  Measurements of the motions would be the same except that the motion of the vehicle must be added or subtracted to be identical to what the other observes and measures.

Symmetry, Noether's theorem & Conservation Laws

Galileo's principles of relativity describe a kind of symmetry in nature where any event must look equivalent to two observers.  This concept has been greatly expanded by later physicists who have used such symmetry as a guide for further discoveries.  (Amalie) Emmy Noether (German pronounced 'nø:té, ←photograph at left, b1882, d1935) proved in 1915 two deep theorems, and their converses, on the connection between symmetries and conservation laws which were subsequently published in 1918.  The first states that any symmetry of an action of a physical system (which has a mathematical description which can be differentiated) has a corresponding conservation law.  Noether's theorems are not in the mainstream of her scholarly work, which was the development of modern abstract algebra.  Instead her help was requested to solve what Albert Einstein and several of their colleagues felt might be a failure of local energy conservation in the general theory of relativity which they had been developing.  Her theorems eliminated that concern and became a fundamental tool of modern theoretical physics.

There are now many such conservation laws.  For examples, time translation symmetry gives conservation of energy; space translation symmetry gives conservation of momentum; rotation symmetry gives conservation of angular momentum (which will be described in subsequent experiments).  Such laws are powerful devices for both understanding what can and cannot occur in the universe and for making useful predictions.  Noether's theorems also were instrumental in the great discoveries of gauge field symmetries of the 20th century which led to our Standard Model of matter.

Reference

• George Sarton, A History of Science: Ancient Science Through the Golden Age of Greece, Wiley, 1952.
• Michael Fowler, Galileo and Einstein, see Selection from Galileo's Dialog Concerning Two New Sciences, University of Virginia and his other materials.
• Nina Byers, E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws, UCLA, 1996