![]()
![]()
As described in Experiment VI-5, Enrico Fermi proposed to his research group in Rome that neutrons, lacking any electric charge, should provide an ideal tool for causing nuclear transformations. Unlike α particles which are repelled as they approach a nucleus, even slow neutrons might approach a nucleus without repulsion, be absorbed, and create a heavier radioactive isotope. Early results in 1934 found silver gained more radioactivity when absorbing neutrons on a wood table than on a marble table. Fermi suspected that neutrons slowed by rebounding off the hydrocarbons in wood were absorbed more readily. The team confirmed the hypothesis by repeating the experiment in the decorative pool of water in front of their building. Soon several European teams were attempting to use neutrons to create an element heavier than Uranium, the largest atom then known.
While neutrons were absorbed creating a radioactive isotope, all teams encountered difficulty chemically identifying the new element produced. In Berlin the chemist, Fritz Strassmann, part of a project started by Lise Meitner and led by Otto Hahn, chemically separated and attempted to identify the new product of
 Meitner, (photo at left) born a Jew, had just narrowly escaped arrest by the Nazis and fled to Stockholm. Just before Christmas 1938, Hahn wrote that when Strassmann used procedures used to collect elements in the Radium family, he isolated a product with the properties of Barium. Hahn asked Meitner to consider the possibility the product was a Barium isotope heavier than Uranium. Walking outside in the snow, Meitner discussed the problem with her nephew, Otto Robert Frisch who had been working with Niels Bohr in Copenhagen. Considering Bohr's liquid drop model of the nucleus, Meitner calculated on a scrap of paper that probably the intermediate nucleus had fissioned producing two radioactive isotopes which could actually include Barium.
Meitner, (photo at left) born a Jew, had just narrowly escaped arrest by the Nazis and fled to Stockholm. Just before Christmas 1938, Hahn wrote that when Strassmann used procedures used to collect elements in the Radium family, he isolated a product with the properties of Barium. Hahn asked Meitner to consider the possibility the product was a Barium isotope heavier than Uranium. Walking outside in the snow, Meitner discussed the problem with her nephew, Otto Robert Frisch who had been working with Niels Bohr in Copenhagen. Considering Bohr's liquid drop model of the nucleus, Meitner calculated on a scrap of paper that probably the intermediate nucleus had fissioned producing two radioactive isotopes which could actually include Barium.
To understand Meitner's proposal it might be helpful to recall the relationship between forces, fields, and energy:
These three descriptions provide different but equivalent perspectives on the same physical effect. Force between objects is easiest for describing the force between two point-like objects. Fields allow people to deal with more complicated situations where a great many objects are located at different distances. Potential energy is most useful for situations where it is too complicated to keep track of all the fields.
Albert Einstein (1879-1955) connected mass with energy by finding the equation E = mc2.
Chemists such as Antoine Lavoisier experimentally found that mass is always conserved so that the total mass never measurably changes during chemical reactions. However measurable amounts of energy are released in exothermic reactions, seeming to contradict Einstein's equation. Calculation using E = mc2 of expected mass change reveals that it was simply too small for chemists to measure. Because an electron's electric charge is tiny, electrical attraction of electrons to atomic nuclei involves small amounts of potential energy.
But accurate measurements of isotope masses revealed that atoms have significant missing mass compared to the sum of masses for constituent protons, neutrons, and electrons. The mass deficit is the equivalent of an object being in a deep hole, held there by gravity unless sufficient potential energy is supplied to hoist the object out of the hole. The mass deficit is a measure of the nuclear binding energy holding the atom together. The nuclear force holding the nucleus together is orders of magnitude greater than the electrical force holding the atom's electrons. Most interesting is a graph of the missing mass per nuclear particle:
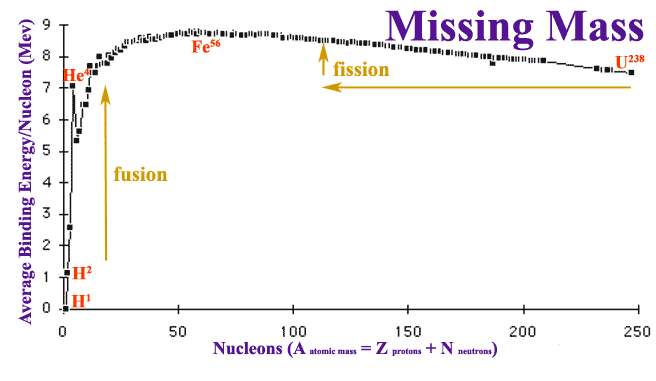
Hydrogen, 1H, is composed of a single proton in the nucleus, precluding any nuclear forces. Inside atoms with several nuclear particles, there could be attractions to every other particle as calculated in the table:
| nucleons | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| # of bonds | 0 | 1 | 3 | 6 | 10 | 15 | ... |
| bonds/nucleon | 0 | .5 | 1.0 | 1.5 | 2.0 | 2.5 | ... |
If that were true, the graph should be a straight line with a rising slope of 0.5 bond/nuclide2. But the actual graph of missing mass is not a straight line but peaks with iron, Fe, then gradually declines. This suggests that attractive nuclear forces occur at only short range and become marginal at greater distances.
Because of the short range of the nuclear force, larger atoms are less stable than medium sized atoms. Thus is was plausible to Meitner and Frisch that a nucleus larger than Uranium might actually oscillate like a shimmering liquid drop then break into two pieces. As noted on the graph, the pieces roughly half as large would have MORE missing energy than Uranium, an amount of energy just matching that Meitner calculated the repelling pieces would generate. It was this agreement between missing mass and the potential energy available due to electrical repulsion that convinced Meitner. After Christmas, Frisch returned to Copenhagen and told Bohr about fission. Bohr then took the news across the Atlantic to an international meeting in New York. Almost immediately physicists realized that the roughly 200 MeV of energy released might be used for making an atomic bomb if enough neutrons were released to carry on a chain reaction. Enrico Fermi, who had used the occasion of receiving the 1938 Nobel Prize to emigrated to America to escape Mussolini, did experiments which confirmed the possibility of a chain reaction. By August 1939 Leo Szilard had drafted a letter (read a copy of the letter) which Albert Einstein signed and sent to U.S. President Roosevelt recommending support for further research.
 Moving to the University of Chicago, Enrico Fermi (shown with wife, Laura) headed construction of a graphite pile to demonstrate that neutrons emitted from fissioning Uranium could be slowed by collisions, then subsequently absorbed, producing controlled chain fission. That demonstrated, Fermi supervised the design and construction of large nuclear fission reactors at Hanford, Washington. (Download and listen to many of the original scientists discuss the discovery of fission. 36 minutes from American Institute of Physics)
Moving to the University of Chicago, Enrico Fermi (shown with wife, Laura) headed construction of a graphite pile to demonstrate that neutrons emitted from fissioning Uranium could be slowed by collisions, then subsequently absorbed, producing controlled chain fission. That demonstrated, Fermi supervised the design and construction of large nuclear fission reactors at Hanford, Washington. (Download and listen to many of the original scientists discuss the discovery of fission. 36 minutes from American Institute of Physics)
Not all attempts to make atoms heavier than Uranium had failed. Efforts by Edwin McMillan and Glenn Seaborg at the University of California, Berkeley, to use Ernest Lawrence's cyclotron to collide slow neutrons and later deuterons with an Uranium target produced submicroscopic amounts of elements 93 and 94, named Neptunium and Plutonium after the recently discovered planets.
The Hanford nuclear reactors Fermi's team designed were optimized to make large amounts of the artificial element Plutonium. The Plutonium was then used to construct one of two atomic bombs which, when exploded in Japan, ended World War II. Today nuclear reactors around the world are instead design optimized to produce a significant fraction of the world's electricity. While intensely radioactive (β emitting) wastes are produced, these compact wastes can be readily contained compared to vast amounts of CO2 (a greenhouse gas) released by production of electricity using carbon fuels.
The rapid rise of the graph of missing mass for the first few elements suggested that a fusion reaction combining light elements to make heavier ones would be extremely exothermic. A number of physicists, knowing that stars are composed mostly of Hydrogen and Helium, speculated that energy of starlight is likely the result of Hydrogen fusing to Helium. After World War II, the United States developed a Hydrogen bomb powered by fusion which is much more powerful than an atomic bomb.
Efforts to find other elements heavier that Uranium in the debris from atomic and Hydrogen bombs found several additional new elements. But as predicted by the drop model of the nucleus, larger nuclei were less tightly bound together, were unstable with briefer existences called half lives (defined as the median period of existence, the time elapsed until half decayed).
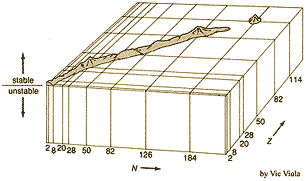 But a three dimensional graphs of the missing mass per nucleon plotted verses an isotope's number of protons (Z) and neutrons (N) revealed periodic ridges and peaks suggesting that nuclei have a quantized shell structure similar to that of electrons in atoms. Certain magic numbers of electrons filled quantum energy levels of atoms resulting in inert elements and stable ions. It appeared that similar magic numbers of protons and neutrons make nuclei more stable. The question arose in the early
But a three dimensional graphs of the missing mass per nucleon plotted verses an isotope's number of protons (Z) and neutrons (N) revealed periodic ridges and peaks suggesting that nuclei have a quantized shell structure similar to that of electrons in atoms. Certain magic numbers of electrons filled quantum energy levels of atoms resulting in inert elements and stable ions. It appeared that similar magic numbers of protons and neutrons make nuclei more stable. The question arose in the early sixties
whether quantum shell effects in nuclei much heavier than Uranium could cause them to be stabilized enough that they might still occur in trace amounts in nature, or could be synthesized. A configuration with two magic numbers, similar to 20882Pb (with 82 protons & 126 neutrons), was anticipated for the isotope 298114X (with 114 protons & 184 neutrons). Calculations in 1966 predicted an island of stability in this region. GSI was founded in Germany in 1969 to build a UNiversal heavy Ion Linear ACcelerator (UNILAC) to systematically investigate all nuclear reactions that could conceivably produce superheavy elements.
Efforts they call cold fusion collide stable ions and atoms typically producing a new atom and a single neutron. More recent efforts using hot fusion collide stable ions with radioactive superheavy elements producing a new atom and four or five neutrons. While only a single atom is produced at a time (at rates of only a few a day), teams at GSI have developed methods of investigating the chemical properties of the atom and its compounds during its brief existence.
 In 1952 Donald Arthur Glaser (b. 1926, Cleveland), replaced the saturated air in cloud chambers with a liquid on the verge of boiling, improving the resolution of the tracks made visible. In such a bubble chamber, the formation of bubbles would scatter light much like the droplets in a cloud chamber. If extremely cold liquid Hydrogen was used, occasionally the radiation collided with the Hydrogen, revealing clues about the interactions between the elementary particles which constitute matter. They also provide evidence about the properties of elementary particles and their decays. Bubble chamber photographs have been used to make many important discoveries and measurements.
In 1952 Donald Arthur Glaser (b. 1926, Cleveland), replaced the saturated air in cloud chambers with a liquid on the verge of boiling, improving the resolution of the tracks made visible. In such a bubble chamber, the formation of bubbles would scatter light much like the droplets in a cloud chamber. If extremely cold liquid Hydrogen was used, occasionally the radiation collided with the Hydrogen, revealing clues about the interactions between the elementary particles which constitute matter. They also provide evidence about the properties of elementary particles and their decays. Bubble chamber photographs have been used to make many important discoveries and measurements.
A single high energy particle may interact with matter in several ways: Passing close by, a portion of its energy and momentum may be transferred to particles in the target. Newly ejected particles leave diverging forked tracks except that any particle without electric charge leaves no track at all. If energy is great enough, interaction may transform energy into a pair of particle and its anti-particle (E = mc2) which in the presence of perpendicular magnetic fields curl in opposite directions. Or the radiation might pass through the matter without any interaction. Thus an uncharged particle that rarely interacts with matter could be extremely hard to discover.
While cloud chambers of condensing vapor and bubble chambers of boiling liquids have been retired and replaced by faster detectors, archived photographs from such chambers still provide visual insights into the nature of high energy particles and the procedures we still used to learn about the particles' properties and interactions. Today such tracks are electronically detected then presented on computer screens looking much like the older photographs. So understanding the imaging processes and studying the particle tracks can help us understand the nature of matter.
To understand some of the behaviors of elementary particles it might be helpful to review what was learned earlier about electromagnetic force: Electric force bonds electrons to atoms. Adding energy to those atoms can create quantized excited states which decay releasing photons of the spectra for that atom. Various rules must be followed, but typically such exited states decay rapidly in 10-16 seconds or so. (Removed from the energy in a flame, atoms immediately stop glowing!) Similar events were observed to occur with particles such as protons that experience the nuclear force which make atomic nuclei stable. These particles called baryons can be excited to various quantized excited states which decay more rapidly in only about 10-23 seconds. This is consistent with a stronger force being able to act more quickly. It was also clear that electrons are not bound by the stronger nuclear force (electrons are not baryons) but are involved in slower β decays. Therefore there is likely a weaker force. which requires a longer 10-10 seconds to decay. The tracks in cloud chambers and bubble chambers provided evidence that the strong force causes changes so rapidly that particles have little change to move, while the particles often leave tracks of considerable length waiting for a weak decay to occur.
But in 1947 cloud chamber photographs below lead struck by cosmic rays revealed forked tracks not caused by later secondary collisions but recording delayed decay of baryons. Expected to rapidly decay while still inside the lead, these baryons travelled much further than expected before decaying. In 1953 Murray Gell-Mann in the United States and Kazuhiko Nishijima in Japan independently proposed that these baryons had a strange quantum property which was conserved by the strong force (thus precluding the strong force from acting with its characteristic quickness), but could be changed by the weak force. Thus the strong force could rapidly create (in collision with lead) a strange particle and another with opposite strangeness (so total strangeness =0), but once parted, each strange particle could only be decayed using the slower weak force. Later, other quantum properties were also discovered.
This experiment involves a few photographs taken at the 2 meter bubble chamber at CERN near Geneva. The pictures were recorded in a bubble chamber filled with liquid hydrogen exposed to a "beam" of negative kaon particles (K-) each with the same momentum. Each picture shows a small region of the chamber (about 20 cm in length) so the distance on the screen is roughly the actual distance in the chamber. The paths of fast moving charged particles in the chamber leave a trail of bubbles which appear as small dots on the photograph.
The superheated liquid in the bubble chamber is prepared by starting with the very cold liquid under pressure (about 5 atmospheres and 3K) and then, just before the particle beam arrives, the pressure is reduced suddenly by expanding the volume by about 1% by means of a piston. After the particles have passed through the liquid, the bubbles expand until they are a few tenths of a millimeter across before being photographed by flash illumination. To enable the reconstruction of the event in three dimensions, photographs from different perspectives are taken using several cameras. The relativistic particles cross the few meters of liquid in a few nanoseconds (1ns = 10-9s); the necessary growth time of the bubbles is about a million times longer, about 10ms. Once the multiple view photographs are taken, the bubbles are collapsed by recompressing the liquid to prepare the bubble chamber for another shower of particles. This process requires a few seconds limiting the speed of the research. The analysis of photographs is labor intensive thus requiring much additional time and funding. The detectors that now replace cloud chambers and bubble chambers can be recycled much more rapidly and their output is computer analyzed allowing searches for much rarer events.
The kaons shower is made by beam of protons from the CERN accelerator collided with appropriate energy into a target. After other particles are removed from the beam, the Kaons typically pass through the mainly empty spaces within each hydrogen atom in the bubble chamber without much interaction. The beam particles are a mixture of neutral and negatively charged. The negative particles curve slightly in the magnetic field of 1.78 Tesla and leave bubble trails. Because they all have the same initial direction and momentum and are travelling in a uniform magnetic field, their track curvature and direction should be the same. Neutral particles do not generate strong magnetic fields which transfer energy needed to create bubbles. So neutral particles do not leave a visible trail. But their presence may be surmised if they decay to charged particles within the bubble chamber or if the visible particles' total of energy and momentum is short. Most uncharged Kaons pass invisibly through the chamber. Occasional cosmic rays or other particles produced outside the bubble chamber also pass through the chamber but typically not parallel to the shower of beam particles.
When a beam particle of just sufficient energy collides with a proton, the kinetic energy of the center of mass can be converted into additional mass (if E = mc2) producing extra particles equal the energy. The number and type of particles produced must be consistent with the conservation laws of the strong force. These include momentum, energy, charge, strangeness, baryon number and lepton number conservation. As the beam (K-) particle is strange (so assigned strangeness =-1) and the proton his not strange (strangeness =0), the produced particles must also have a total strangeness of -1. Because the target proton is a baryon (i.e., baryon number =+1) and the beam K- is a meson (not a baryon, so baryon number =0), the produced particles must have a total baryon number of +1.
The electron and it antiparticle called positron have a much smaller mass than other particles. When they experience electromagnetic forces they are accelerated more than more massive particles leading to a more rapid loss in their energy by radiation of photons. This rapid loss of energy results in the characteristic tight decreasing spiral of an electron (or positron) track.
It is often difficult to use the track properties to distinguish between different particles. However the large mass of the proton means it can sometimes be clearly identified by the density of bubbles (or darkness) of the track. The number of bubbles per centimeter is inversely proportional to the square of the particle velocity. Where two particles have similar momentum then the velocity of a particle will be inversely proportional to its mass. As the proton is the heaviest stable particle and is around seven times heavier than the pion its bubble density will be around fifty times larger than a pion. Consequently the darkest tracks are typically caused by protons.
The walls of the chamber are marked with "X"s to facilitate three-dimensional reconstruction of a collision using simultaneous pictures from several perspectives. The photographs selected for our use were selected because the recorded events which lie is primarily the plane perpendicular to the camera so that only a single two-dimensional camera view is needed for our analysis.
This experiment has been deliberately structured into two different tasks. After a short introduction to common features of the photographs you are asked to examine the main features of each photograph and identify the types of particle interactions and decays that occur.
Later some pictures are revisited so you can extract even more information using advanced concepts. Some particles only exist for 10-23 seconds so they do not leave a measurable track in the bubble chamber even when travelling a speed equal that of light. They can only travel a distance equal to the diameter of a proton before decaying. Yet with advanced concepts their presence can be detected and their properties measured.
If necessary, use this link to open the second photograph.
The negatively charged beam kaon interacts with the positively charged proton at h to produce positive, negative and a neutral particle.![]()
next Experiment
to ie-Physics menu
to site menu