![]()
![]()
It is not unusual to want to know information that we can't observe directly. Intelligent beings such as ourselves often can devise methods to obtain the desired information. For example, when Galileo Galilei (1564-1642) while a university teacher in Venice, Italy, heard about a device assembled in Holland to magnify one's view, he built such a telescope and viewed the Moon. Seeing rough features which he believed to be mountains and valleys much like the rugged surface of Earth, he devised a method and measured the height of a Moon mountain he named Piton.
Previously Nicholas Koppernigk (born 1473 at Thorn on the Vistula in what eventually became Poland, died 1543 before Galileo's birth), a cannon (lawyer) for the Christian Church in Prussia, and amateur astronomer, had been concerned that God would not have created the universe to have irregularities such as the equant which Ptolemy had used to speed and slow the motion of planets. So Copernicus (as he Latinized his name) developed an alternative explanation for heavenly motions. Copernicus admitted that Ptolemy's model for the universe did accurately explain all motions and changes of brightness in the heavens. But he believed that God made the heavens perfect in every respect. Seeking to correct what he viewed as Ptolemy's flaw, he realized if epicycles were added to Aristarchos' model of the heavens, the daily motion of the celestial sphere and many of Ptolemy's epicycles would be unneeded. Instead the Earth would be a planet orbiting the Sun just like the other planets. To avoid the need for the imperfect equant, Copernicus had to add as many as seven successive epicycles for some planets. To explain why stellar parallax has not been observed as predicted by Aristarchos' model, Copernicus suggested the stars had to be enormously distant so that the parallax was too small to notice. The retrograde of planets was explained by an inner planet passing the Earth or the Earth over taking and passing another planet. Never the less, Copernicus was able to propose a system of perfect circular motions that could explain every heavenly motion equally well as Ptolemy's model.
Copernicus' model was widely discussed by astronomers, many whom believed the lack of any evidence for the Earth's motion still made Ptolemy's explanation better.
Galileo however generally disliked the idea that the ancient Greeks could have done no wrong. He liked Copernicus' claim that Ptolemy's explanation contained an imperfection. So when Galileo observed with his new telescope mountains and valleys on the Moon, he viewed that as evidence of further imperfections in what the ancients viewed as perfectly spherical heavens. Galileo wrote:Galileo continued his observations of the sky with his telescope discovering that Venus had phases of darkness just like the imperfect Moon, the Sun had spots, Saturn had what looked like ears, and four small moons orbited Jupiter demonstrating that not all heavenly bodies moved with the earth as the centers of their rotation. Armed with this evidence, Galileo embarked on a drive to convince everyone that the Greeks had flawed ideas that needed to be updated.Let me first speak of the surface of the Moon, which is turned towards us. ...I distinguish two parts in it, which I call respectively the brighter and the darker. ...but the darker part ...discolors the Moon's surface and makes it covered with spots. Now these spots, as they are somewhat dark and of considerable size, are plain to every one, and every age has seen them, wherefore I shall call them great or ancient spots, to distinguish them from other spots, smaller in size, but so thickly scattered that they sprinkle the whole surface of the Moon. These spots have never been observed by anyone before me; and from my observations of them, often repeated, I have been led to that opinion which I have expressed, namely, that I feel sure that the surface of the Moon is not perfectly smooth, free from inequalities and exactly spherical as a large school of philosophers considers with regard to the Moon and the other heavenly bodies, but that, on the contrary, it is full of inequalities, uneven, full of hollows and protuberances, just like the surface of the Earth itself.
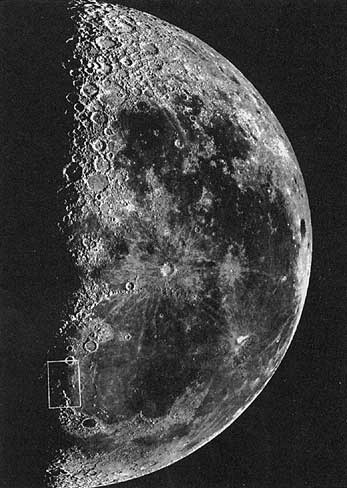
To the right is a photograph of the Moon taken through a telescope. Because the Sun is illuminating the Moon from 90° from our line of sight, there is a terminator dividing the lit half from the dark half. Galileo noted that this terminator is not a perfectly smooth line:
...the boundary which divides the part in shadow from the enlightened part does not extend continuously in an ellipse, as would happen in the case of a perfectly spherical body, but it is marked out by an irregular, uneven, and very wavy line (with) ...several bright excrescences ...beyond the boundary of light... and on the other hand pieces of shadow encroach upon the light.
Now I have noticed that the small spots ...have this common characteristic ...that they have the dark part towards the Sun's position, and on the side away from the Sun they have brighter boundaries, as if they were crowned with shining summits. Now we have an appearance quite similar on the Earth about sunrise, when we behold the valleys, not yet flooded with light, but the mountains surrounding them on the side opposite to the Sun already ablaze with the splendor of his beams; and just as the shadows in the hollows of the Earth diminish in size as the Sun rises higher, so also these spots on the Moon lose their blackness as the illuminated part grows larger and larger. ...Now, is it not the case on the Earth before sunrise, that while the level plain is still in shadow, the peaks of the most lofty mountains are illuminated by the Sun's rays?
Near the bottom of the Moon is a rectangle indicating a section of the photograph shown below magnified 10 times larger.
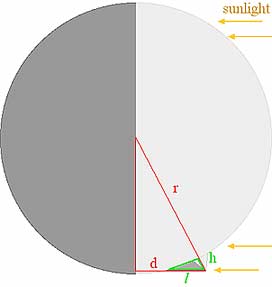
This diagram shows the moon rotated downward until Piton and its shadow are in silloette. We can construct a red right triangle using the Moon's radius, r,
and the distance between Piton and the terminator, d.
We can also construct a smaller green right triangle using the length of the shadow, l,
and the height of Piton, h.
These are similar triangles because the share a common angle and the right angle. Therefore we can establish a ratio between similar sides: h / l = d / r.
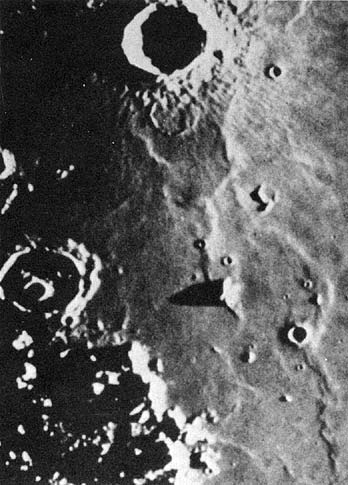
r.Multiple by 10 so your measurements are on the same scale as the enlargement at right.
l.
d.This may be the least accurate measurement. It may be easiest to determine the location of the terminator extending vertically on the screen by looking for where darkness begins out in the flat lunar plains.
h.is the height of Piton. Substitute and determine the apparent height of the mountain as if the photograph was three dimensional.
How does the height of Piton compare to the height of typical mountains on Earth?
Finally, record your procedures, measurements, and findings in your journal. If you need course credit, use your observations recorded in your journal to construct a formal report