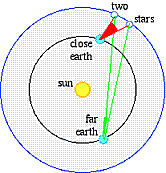ie-Physics

Experiment II-3

If Aristarchos was correct and the Earth did orbit the Sun, then there should be confirming evidence both here on Earth, and with careful observations of the sky.  If the Earth moved, the motion would likely be felt.  If the Earth moved the motion would likely cause strong prevailing winds from the direction of motion.  But more fundamentally, if the Sun occupied the center position and the Earth orbited the Sun, then the angle between neighboring stars along the ecliptic should change with the seasons.  When the Earth was closer to the stars the angle should be larger, but when the Earth orbited farther from the stars the angle between the stars should decrease.  The lack of any such observable parallax, the lack of any prevailing winds, and the lack of any other evidence of earth motion led the Greeks to reject Aristarchos' proposal that the Earth orbited the Sun.

Eratosthenes of Cyrene (b 273 BC, d 192 BC) masterfully measured the size of the earth (using the technique explained below).  Eratosthenes was born in Cyrene, the capital city of the region west of Egypt.  He was educated in Athens, which was still the educational and philosophical center of the Mediterranean despite the rise of the Roman empire.  After distinguishing himself academically, he was recruited by the Ptolemaios to tutor a prince in Alexandria, Egypt.  Ten years later he became the chief librarian of the Museum of Alexandria, a job that went beyond supervising the vast collections to include leading for four decades the extensive scientific research sponsored by that institution.  While he excelled in many areas, Eratosthenes became one of the greatest geographers of all ages by establishing the mathematical geography of the spherical earth, including a system of latitude and longitude.

A number of astronomers catalogued the visible stars.  The most thorough catalog was by Claudius Ptolemy of Alexandria (b 87 AD Egyptian but still in the culture of Greece, d 150 AD).  Ptolemy must have had one of the greatest minds of all time.  He wrote books on optics, geography, astronomy, and astrology that each became the primary source of information for that subject for over 1000 years!  The Tetrabiblos on astrology is still used today!  His Mathematical Syntaxis on astronomy became known in the Arab world as the Almagest, meaning simply the greatest, the title it is still know by today.  By Ptolemy's time it had been noted that the planets get brighter while they retrograde, a feature that Eudoxos' concentric spheres did not explain.  Ptolemy simplified that theory by noting that the motion of an object attached to a sphere is merely a circle.  In his theory:

1. The celestial sphere continued to carry all heavenly bodies around the earth each day.
   
   
2. According to Ptolemy, the primary motion of each planet is due to its deferent, a circle rotating about the Earth.
   
   
3. Retrograde is due to a secondary circle called an epicycle with its center attached to the deferent and rotating the same direction.  (Recall that Eudoxos used two connected concentric spheres, each moving with uniform circular motion.)  The planet is attached to the epicycle so as it swings to the outside of the deferent on its journey backwards compared to the stars, it grows fainter due to greater distance.  But when the epicycle swings the planet inside the deferent, the epicycle's greater speed counteracts the deferent motion so while the planet is close and bright, for a few days it retrogrades, moving faster across the sky than the stars.
   
   
4. To adjust the speed of the perfect circular motion of the deferent to match the actual planet, Ptolemy moved the Earth slightly off center and added another point called an equant, equally off center the other side of the deferent's center.  The deferent rotates with uniform angular speed around the equant so the deferent seemed to alternately slow then speed as viewed from Earth.

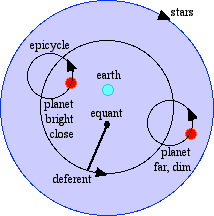
Ptolemy's deferents, epicycles, and equants could explain all motion as well as Eudoxos, but could also explain all observed variations in brightness.  Again the Greeks had managed to explain all the known observations of the heavens.

Experiment:
Measure the Size of the Earth

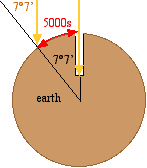
Eratosthenes learned that at the summer solstice along the Nile river in the town of Syene (now Aswan), the Sun at noon shown straight down a deep well, casting no shadow on the walls.  But in Alexandria, a measured distance of 5000 stadia down river to the North (the Egyptians used geometry to survey, measure and map the Nile valley for farm management), the Sun was 1/50 of a great circle (360° / 50 = 7° 7') away from overhead.  Thus the Earth's circumference would be 50 times this distance!  Using this information, determine the circumference and diameter of the Earth.  If the stadium Eratosthenes used as his standard of measurement was 160 meters (most stadia in the Greek world have been destroyed, but this seems a reasonable estimate based on archeology), what is the diameter of the Earth by today's standard, the meter?

If you can arrange with someone living a known distance north or south of you, both can measure the highest elevation of the Sun on any same day, then repeat the the calculations for your own data.  (Use caution to avoid looking directly at the Sun.)

Again we should note that the Greeks relied heavily on careful observations, the a priori method, and deductive logic to solve apparently difficult problems.  These tools of science are still widely used today.

References

• George Sarton, A History of Science: Ancient Science Through the Golden Age of Greece, Wiley, 1952.
• George Sarton, A History of Science: Hellenistic Science and Culture in the Last Three Centuries B.C., Wiley, 1959.
• O. Neugebauer, The Exact Science in Antiquity, Princeton U. Press, 1952.