Isaac Newton's 1687 mathematical description of gravity nearly perfectly accounted for all of the then observable heavenly motions. Two centuries later, Albert Einstein detected a problem in viewing electrical and magnetic phenomena from moving and stationary perspectives and develop Special Relativity as the solution. Einstein later added gravity into a broader solution which he called General Relativity. Einstein suggested that General Relativity required small variations in heavenly motions from Newton's descriptions. These were eventually measured, confirming the validity of General Relativity.
The very creative maverick, but often offensively brash Fritz Zwicky (b1898 in Bulgaria, d1974 shown at right→) studied physics at the ETH in Zürich and produced a dissertation there under the guidance of Nobel chemist Peter Debye. Zwicky was recruited to work on crystal structure at CalTech by physicist Robert Millikan, its Nobel winning president. Zwicky, who thrived on investigating and theorizing about extreme phenomena, became interested in astrophysics. Zwicky helped promote the Mt. Palomar telescopes which he later used to map out hundreds of thousands of galaxies. Zwicky was the first to notice that galaxies tended to cluster. The orbital speeds of galaxies in a cluster depend on the mass of the cluster, since each galaxy is attracted by the gravity of the others closer to their common center. From the observed speeds of outer galaxies moving around the Coma cluster (based on Dopper shifts of their spectral lines), Zwicky calculated total mass of the cluster. In 1933 he compared that to an alternate method of finding a mass of a cluster by summing the light from the galaxies in the cluster. Based on the amount of light emitted from stars of known mass much closer to us, Zwicky used the total amount of light emitted from the cluster to calculate the mass of the of all the stars in the cluster emitting that light. Finding the masses of the light emitting stars to be only 1/10 to 1/100 of what was needed to maintain the galaxies in a stable cluster, Zwicky speculated the existence of additional matter in the cluster not emitting light, what he termed dark matter. The nature of this dark matter was unclear to Zwicky and his contemporaries and continues to be an enigma today. (He and friend Walter Baabe proposed that supernovae are caused when stars collapse to neutron stars, generating cosmic rays. Zwicky proceeded to discover more supernovae than anyone else: 120. Zwicky was also responsible for the concepts of supernovae, neutron stars, and gravitational lenses. He helped develop modern jet and rocket engines, and more.)
Vera (Cooper) Rubin (b1928 in Philadelphia, shown at right→) was an undergraduate at Vassar College, before earning a masters degree from Cornell University, studying with physicists Philip Morrison, Richard Feynman, and Hans Bethe. She next earned a doctorate at Georgetown University from George Gamow. She later taught at Georgetown while raising four children, all earning doctorates in math or sciences. Although physicists firmly believed that the mathematics of gravity (F = G m1m2 / d2) requires orbit speeds similar to what was first observed by Kepler (3rd Law), there was difficulty confirming that outside our solar system. The brighter area in the center of most galaxies suggests most mass is there. Just like in our solar system, the stars and other objects closer to the concentration of mass at each center should orbit faster than in the less luminous outer arms at the edge of each galaxy. If the mass near the center moved faster and that near the edges moved slower, a graph of the velocities verses distance from the galactic center should be a declining curve showing less velocities far out. Jan Oort had found that velocities in the Milky Way galaxy do not decrease with increasing distance from the galactic center as expected. But much of the Milky Way is obscured from measurement by dust resulting in considerable uncertainty about the distribution of mass in our galaxy.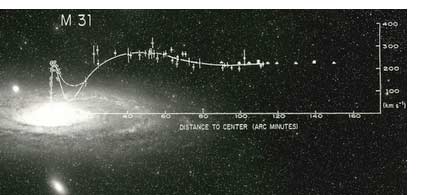 
Vera Rubin and Kent Ford studied spectra of stars in our neighboring Andromeda galaxy and found nearly a flat line graph of orbit speed versed distance from galactic center. (Velocities calculated from visible spectra of ionized gas clouds, the open and filled circles, and from neutral Hydrogen radio spectra, the filled triangles, are ←at left imposed to scale on a photograph of the Andromeda galaxy, M31. Note that the velocities remain high far beyond the visible disk of M31.) Rubin's team then made observations of over 60 other spiral galaxies which confirmed that such flat graphs extend as far out as any galaxy seems to go. Recalling the measurements of clusters of galaxies made by Fritz Zwicky three decades earlier, Rubin realized that the missing mass inside galaxies could be what Zwicky called dark matter in clusters of galaxies. Since 1978, Rubin and her team at Carnegie Institution in Washington have analyzed more than 200 galaxies. They estimate that at least 90% of the universe is made of dark matter which can be neither the glowing chemical elements which compose stars or the cold clouds of mostly Hydrogen and Helium which extends beyond but still exhibit their tell-tale atomic absorption spectra.
A number of diverse studies have confirmed that the matter previously known to chemists and physicists cannot be the mysterious dark matter. 2003 measurements using the WMAP satellite of the polarity of cosmic microwave background radiation (residual radiation much cooled and red-shifted from the Big Bang) carried implications about characteristics of the early universe including the density of dark matter. That study found that dark matter composes 90% of the total mass of the universe, leaving only 10% composed of the atoms and molecules understood by chemists and the particles of physicists' Standard Model.
But the first direct evidence that dark matter must exist was presented August 2006 by groups led by Maxim Markevitch and Douglas Clowe. Markevitch's group used the Chandra X-ray telescope to detect shocked gaseous atoms (shown pink dimming through purple to black on the X-ray+visible+map montage ←at left) 4 billion light years away emerging from a collision 150 million years earlier between the Bullet cluster (1E0657-56) with another cluster in the constellation of Carina. A classic > shaped bow shock wave in the gas of the smaller Bullet cluster (pink on right), allowed determination of the velocity of the cluster (4500 km/s) and its direction of motion (to right on montage).
Clowe's group analyzed visible light photographs from the Hubble Telescope. Gravitational lensing distorts the shapes of the (white) background galaxies by gravitationally deflecting light as it passed by the mass of these two colliding clusters. Clowe's group was able to use the distortions to map the distribution of mass in the clusters (as the green topographic overlay). With the pinched central region, it clearly shows the locations of the mass of the two clusters emerging from their collision.
Carried by their momenta, dense stars generally passed through the largely empty space of the other galaxy with little change of velocity. But the bulk of the clusters' ordinary matter, the clouds of gas encompassing each galaxy, were delayed by a drag of the passing mass of the other galaxy. A very small minority of those atoms disclosed the location of their clouds when they were excited by collision with atoms in the other cluster. The X-rays were emitted as each excited atom calmed after its shocking collision. The critical evidence is that the (pink) gas clouds are not centered with cluster masses as would be expected if the clusters were composed of ordinary atoms and other standard matter! If dark matter didn't exist, the bulk of the mass would remain centered with the gas clouds. The gas clouds separation from most of the clusters' mass gives the best evidence that most of the mass must be due to some form of dark matter. The alternate explanation, that missing mass is instead due to a flaw in our understanding of gravity, seems unable to account for these new observations. The evidence shown here suggests that the dark matter didn't experience the drag of the collision.
While there are a number of theoretical proposals attempting to provide an understanding of dark matter, currently we know little beyond the need for dark matter to exist.
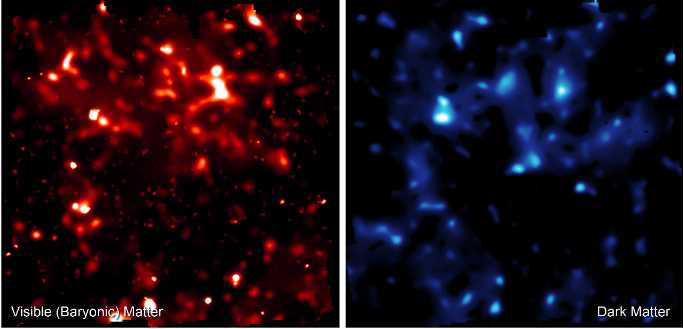
Astronomers used the Hubble Telescope to create the first 3-dimensional map of a patch of dark matter in the universe. Ordinary matter (such as protons and neutrons) account for only about 1/6 of the total matter in the Universe. The remainder is a mysterious dark matter, which does not interact via electromagnetism and so neither emits nor reflects light. Since dark matter cannot be seen directly, very little is currently known about its properties. It does interact via gravity, so its distribution in the sky is most effectively studied through gravitational lensing, the slight deflection of the paths of light from distant galaxies by the gravitational attraction of nearer masses. This is a purely geometrical effect that is free of astrophysical assumptions and sensitive to all matter, whether ordinary or dark.
Researchers created the map as a part of the Cosmic Evolution Survey, otherwise called COSMOS. The survey covers an area of sky nine times the area of the Earth's moon. The catalog is constructed from 575 ACS/WFC tiles (1.64 deg2) and contains a total 1.2x106 objects to a limiting magnitude of F814W=26.5. The final COSMOS weak lensing catalog contains 3.9x105 galaxies with accurate shape measurements. The distances to the galaxies were determined from their spectral redshifts, using the Subaru telescope in Hawaii. The distribution of additional gas outside galaxies was measured with the European Space Agency's XMM/Newton telescope. The map stretches both in distance and time halfway back to the beginning of the universe, revealing how dark matter has grown increasingly clumpy
as it collapses under gravity.
These two false-color images compare the distribution of visible normal matter (←red) with dark matter (blue→) with brightness corresponding to clumps of mass. This map provides evidence that normal matter, largely in the form of galaxies, accumulates along the densest concentrations of dark matter. The map reveals a loose network of dark matter filaments which grew over time and intersect in massive structures at the locations of clusters of galaxies.
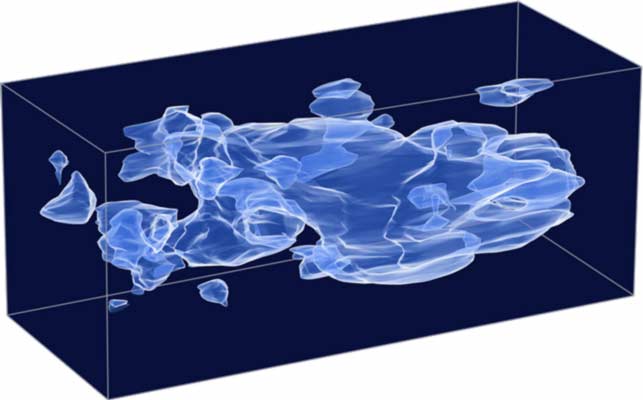
Combining the distance information obtained from the specta of the galaxies with the location of the dark matter based on gravitational lensing, a three-dimensional map of dark matter was produced. Because of the finite speed of light, what we presently know of regions further away are revealed by light which originated further back in time. This map stretches halfway back in time to the beginning of the universe. The 3-D map shown below is shown from the vantage of the earth being at left, looking to the right⇒ further away and back in time. Note the map shows the web-like distribution of dark matter. The clumps of the dark matter are more pronounced on the left ⇐, the most recent. This is consistent with predictions of the formation of structure induced by gravity. The loose network of dark matter filaments has been gradually collapsing under the pull of gravity, growing clumpier over time. Starting from a comparatively smooth distribution of matter at the time of the big bang, the dark matter filaments began to form first and, due to their greater mass, subsequently direct the construction of the structure of ordinary matter. Without dark matter, there would have been insufficient mass in the universe for structures to collapse and form galaxies.
A number of experiments have set limits on the properties of dark matter. Physicists acknowledge that dark matter may have properties not yet imagined. But it seems most likely that since it hasn't already been obvious via the typical forces and effects we routinely witness and experience, that dark matter must only weakly interact with the matter (described by the Standard Model) which has been previously discovered. Collisions in particle accelerators which should have made dark matter if it were composed of relatively low mass particles have not produced any detected events. So physicists speculate that dark matter might be composed of weakly interacting, massive particles (WIMPs).
The Cryogenic Dark Matter Search experiment, located a half-mile underground at the Soudan mine in northern Minnesota, has been searching for WIMPs since 2003. The experiment uses 30 detectors made of crystals of Germanium and Silicon. Particle interactions in the semiconductors deposit energy as heat and as electric charges which move in an applied electric field. Sensors detect both these changes, converting them to electrical signals which are amplified and recorded for later analysis. Layers of shielding materials, as well as the half-mile of rock above the experiment, are used to stop most of the background particles. By comparing the size and relative timing of these two signals, experimenters can distinguish whether the particle that interacted in the crystal was a WIMP or a residual Standard Model background particle. So far the experiment has detected two events which seem likely due to WIMPs, with about a one in four chance that these still might be due to background particles. Plans are to improve the detector in 2010 with three times the mass of Germanium and lower backgrounds with the hope of reducing the possibility that such events are caused by anything other than WIMPs. If sufficient additional similar events are detected, the group may eventually be able to confirm the discovery of WIMPs.
As this is being written, it is not clear what experiment will provide us with a deeper understanding of dark matter. Perhaps it is appropriate to consider a procedure for creativity from one of America's most creative scientists: Fritz Zwicky.
"... within the final and true world image everything is related to everything, and nothing can be discarded a priori as being unimportant." (Fritz Zwicky: Discovery, Invention, Research through the Morphological Approach, 1969.)
"Morphological analysis is simply an ordered way of looking at things." (Fritz Zwicky: "Morphological Astronomy", The Observatory. Vol. 68, No. 845, Aug. 1948.)
"...the term morphology has long been used in many fields of science to designate research on structural interrelations - for instance in anatomy, geology, botany and biology. ... I have proposed to generalize and systematize the concept of morphological research and include not only the study of the shapes of geometrical, geological, biological, and generally material structures, but also to study the more abstract structural interrelations among phenomena, concepts, and ideas, whatever their character might be." (Zwicky, 1966, p. 34)
Try applying Zwicky's Morphological Procedure for Non-quantifiable Problems. In picking a problem you may want to consider a distinction between tame and wicked problems:
A tame problem (Conklin, J, 2001, p.11)Wicked problems are completely different. Wicked problems are ill-defined, ambiguous and often associated with strong moral, political and professional issues. Since they are strongly dependent on personal views, there is often little consensus about what the problem is or how to solve it. Wicked problems often won't remain constant: they interact with issues evolving in a changing social context. Often, new forms of wicked problems emerge as a result of approaching understanding or solving one of them. The most evident, and important wicked problems are complex, long-term social and organizational problems. Examples are:
The classical systems approach ...is based on the assumption that a planning project can be organized into distinct phases: 'understand the problems', 'gather information,' 'synthesize information and wait for the creative leap,' 'work out solutions' and the like. For wicked problems, however, this type of scheme does not work. One cannot understand the problem without knowing about its context; one cannot meaningfully search for information without the orientation of a solution concept; one cannot first understand, then solve." (Rittel & Webber, 1974, p. 161)
With that vague guidance, pick a problem and try the method. If you feel totally lost, perhaps start with a simple problem such as:Shall I wear shorts or long pants?Typical issues will be:
Hopefully it is clear that such procedures become much more useful when dealing with more complicated problems. But it is easiest to learn HOW to do a procedure by first using it on very simple problems.
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
to next Experiment
to e-Physics menu
to site menu
