James Clerk Maxwell's equations based on Faraday's fields of lines of force provided a unified theory of electromagnetic phenomena as successful as Isaac Newton's equations for motions caused by gravity and all other forces. But as is always the case, small questions remained to be solved. Little was known about the medium of the fields carrying the electromagnetic waves to us from the farthest corners of the universe, fields which must fill the otherwise vacuum of space. Efforts to investigate this medium, traditionally (since Aristotle's introduction) called the æther, encountered difficulties.
As those difficulties were being investigated, a bright 26 year old Albert Einstein (b1879 in Germany, shown at right at graduation, d1955) pondered the equations of Maxwell and saw a paradox. He discussed the problem and possible solutions with his study mate (and later wife and often silent partner) Mileva. Einstein was the kind of college student who often frustrates teachers by choosing to spend his time trying to develop an intuitive grasp of fundamental ideas rather than cranking out answers to assigned homework. After graduating with lackluster credentials, Einstein could not secure employment in a position appropriate for a competent scientist. But a job as a clerk in the Swiss Patent Office left his evenings and weekends free for continued discussions with Mileva and friends. Maxwell's equations, like Faraday's original lines of force, described that a moving electric charge creates around it a magnetic field. But a stationary electric charge does not. The Einsteins pondered a situation where an observer might accompany a moving electric charge. A sideline observer being passed would detect both an electric field and a magnetic field (say by its effect on a charge held by that observer) but the observer accompanying the moving charge would see the effect as only due to the electric field. How could a magnetic field simultaneously exist and not exist? The equations for the two perspectives must be forced to agree about what is real. And the simplest way to make the equations agree was to assume that all observers must find a common speed at which the information arrived, the speed of electromagnetic phenomena called the speed of light. While that assumption was the simplest solution, it required strange new effects at high speeds approaching the speed of light. Einstein submitted these ideas in a 1905 paper in which he introduces what he called the Principle of Relativity
, now called the Special Theory of Relativity.
The Einstein paper noted that because time is required for information to travel from one observer to the other (at the speed of light, c), we need to carefully consider what we mean by time
and simultaneous events.
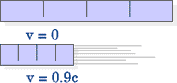
Einstein(s) shows that if we are willing to assume that everyone measures the same speed for light (in a vacuum) even though observers are moving relative to each others, then Maxwell's laws for electricity and magnetism become logically consistent. But this requires that moving rulers are shrunk in the direction of motion (as diagrammed). This also means that the intensity and energy of a light beam will be greater for observers moving towards a source of light. The electric and magnetic forces exerted on a moving charge moving nearly as fast as light would be identical to those on a slowly moving charge. Finally Einstein(s) shows that a mass (such as that of an electron) moving at a speed close to that of light will have increased momentum and energy commensurate with an apparent increase in mass.
Previously in 1887 Albert Michelson and Edward Morley attempted to measure the speed at which the Earth travels through the æther that transports the electromagnetic oscillations. But they failed to detect any effect due to motion of the earth. Poincaré developed an elaborate theory and Lorentz developed equations to attempt to account for this unexpected result. But Einstein's Special Theory of Relativity arrived at the same equations from a single, simpler assumption about the constant speed of light.
While physicists universally accepted the real existence of electric and magnetic fields as presented by Maxwell's equations, Einstein pointed out that there exists no way to learn anything useful about the æther. While it makes little sense to believe in electromagnetic waves without something in space being displaced to carry the waves, the best we can do is the acknowledge that space does transmit such waves. The identical measure of the speed of light in a vacuum for all observers prevents us from knowing more about this aspect of space. Any further discussion of the æther would just waste our time!
In 1937, after nearly a decade of study of cosmic rays and H. Yukawa's 1935 prediction of the existence of a mid-mass particle (meson) responsible as carrier of the nuclear force, S.H. Neddermeyer and C.D. Anderson found evidence in cosmic ray showers of some particles less massive than protons but more penetrating than electrons.
By 1940 it had been determined that these mesotrons were not Yukawa's predicted particle, but rather an unstable particle that rapidly decays into electrons. In 1941 B. Rossi and D. Hall, attempting to measure the lifetime, measured the intensity of mesotrons from cosmic rays, shielded by iron from cosmic rays showers and soft components, both at Denver and nearby Echo Lake (1624 m higher elevation). Rossi eventually determined that mesotrons (now called muons) have an at rest mean lifetime of 2.3 ± 0.2 microseconds
(now accepted to be 2.2 x 10-6 seconds). In 1963 David Frisch and James Smith repeated the experiment at the top of Mt. Washington, the highest peak in the northeastern United States, and at sea level, as a demonstration of special relativity, recording the experiment and results in a movie.
The muons are short-lived particles which are created when higher energy cosmic rays strike the earth's atmosphere. Half of the muons decay every 2.20 x 10-6 second. While the muons are stopped or deflected only slightly by the earth's atmosphere, the muons spontaneously decay at this rate regardless of the physical conditions around them. So their decay occurs as if governed by a very accurate clock that is oblivious to conditions such as temperature that affect many other types of clocks. In this famous Mt. Washington experiment, the number of muon decays which they detected at an elevation of 1910 m, 568 per hour, was compared with the number they detected at an elevation of only a few meters, 412 per hour. The muons travel at nearly the speed of light but they still take a fraction of a second to travel the additional distance from the elevation of Mt. Washington to sea level. As a result some of the muons decay so fewer are counted at sea level. But since the muons are travelling nearly the speed of light, their internal clock is slowed by the amount accounted for by Einstein's special relativity so that more reach sea level than otherwise expected.
Record your observations recorded in your journal. If you need course credit, use the information in your journal to construct a formal report.
On the Electrodynamics of Moving Bodies,translated from
Zur Elektrodynamik bewegter Körperfrom Annalen der Physik, 1905.
to next Experiment
to ie-Physics menu
to site menu
