As long as 2500 years ago people were wondering about the nature of reality. Some speculated that the world was composed of continuous elementary materials while others imagined discontinuous parts called atoms. As noted previously many people had speculated on models to explain some of the strange properties of light. Isaac Newton had proposed that particles of light could explain most observed behavior of light. While Robert Hooke, Christiaan Huygens and Thomas Young had suggested that light behaves more like waves. But Augustin Jean Fresnel's 1818 mathematical wave model provided predictions that when confirmed seemed to clinch the view that light possesses the properties of waves.
The most common light sources are heated objects. But most of them introduce into their color spectra complex effects due to their atoms, interactions with neighboring atoms and their temperatures. To avoid such difficulties, physicists chose to study objects commonly called black bodies. Such objects absorb all entering light so may seem to be perfectly black. The light such black bodies emit depends only on the internal temperature. A kiln with only a small opening to permit observations comes close to being a perfect black body. (When cold the insides of such a cavity looks nearly perfectly black since any light shining into the small opening bounces around inside until absorbed, leaving none to escape. When a kiln is hot, the light leaving is a nearly detail-less uniform glow, free of all chemistry effects and depends only on the temperature inside.) 
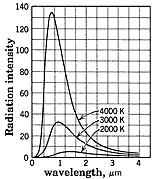As shown on the graph, black bodies emit a range of colors (i.e., different wavelengths) with a peak intensity at a particular color depending on the body's temperature. The total intensity of all emitted radiation, R, depends on the temperature by
A theoretical explanation for shape of these black body radiation graphs eluded a number of capable physicists and remained the major outstanding unsolved problem at the beginning of the twentieth century. The solution to that problem produced an unsettling paradox about the nature of light. When Max Planck (1858-1947) tried to find mathematics to describe the radiation from black bodies, he found that equations derived from the wave properties of light produced graphs that incorrectly peaked at zero wavelength. Planck assumed that the atoms of the cavity walls must act like electromagnetic oscillators which could absorb and emit light. After earlier efforts had failed, Planck tried a common trick used in calculus of treating each atom as if it were only permitted oscillations with an integer multipled by a small constant, h. Planck was hoping to arrive at an equation where the constant could be made vanishing small allowing for all possible oscillations. For calculation purposes each oscillator would have an energy, E = nhν, where n is an integer and ν a frequency of oscillation. Again for purposes of calculation, the oscillator would not emit radiation continuously, but only in jumps or quanta bundles so that the energy radiated would be ΔE = Δnhν. The equation produced graphs that matched the black body radiation but unfortunately the tiny constant, h, remained in his equation. On an afternoon walk with his son he commented he had come upon a discovery as revolutionary as Newton's. In 1900 Planck announced his findings to the Berlin Physical Society and started what has become known as modern physics. This equation seemed to suggest that light could only be emitted or absorbed as discontinuous packages. Planck was never satisfied with this implication and continued to unsuccessfully look for a way to avoid needing this quantum requirement. Never the less, Planck was awarded the 1918 Nobel Prize in Physics for his quantum theory.
Previous in 1887 the German physicist Heinrich Hertz had noticed when testing Maxwell's theory of electromagnetic radiation that sometimes light can kick electrically charged particles from the surface of some metals. In 1898 J.J. Thomson measured the charge to mass ratio of these photoelectric effect particles and found them to match the cathode rays boiling off hot cathode (negatively charged) wires. These particles, now called electrons, can be counted by collecting them on a metal plate and conducting them through a sensitive ammeter. The energy of these electrons can also be measured by repelling them from the detector by applying a positive voltage. As repelling voltage is increased, gradually fewer and fewer electrons have enough kinetic energy to reach the detector plate and be counted. The voltage needed to prevent any electrons from being detected is a direct measure of the energy of the most energetic of electrons: KEmax = V / qe where qe is the charge of an electron. Measuring the kinetic energy of the electrons ejected by light via the photoelectric effect led to three troubling findings:
In 1905 Albert Einstein (1879-1955) recalled Planck's paradox and used it to explain the troubling photoelectric effect properties. He suggested that not only was light emitted and received by atoms in quanta, but that light itself exists as quanta. He wrote:
...according to the idea that the incident light consists of quanta with energy hν, the ejection of cathode rays by light can be understood in the following way. Energy quanta penetrate the surface layer of the body, and their energy is converted at least in part, into kinetic energy of electrons. The simplest picture is that a light quanta gives up all its energy to a single electron; we shall assume that this happens. The possibility is not to excluded, however, that electrons receive their energy only in part from the light quantum. An electron provided with kinetic energy inside the body may have lost part of its kinetic energy by the time it reaches the surface. In addition, it is to be assumed that each electron, in leaving the body, has to do an amount of work W (which is characteristic of the body). The electrons ejected directly from the surface and at right angeles to it will have the greatest velocities perpendicular to the surface. The maximum kinetic energy of such an electron isKEmax = hν - W If the body plate C is charge to a positive potential, Vstop just large enough to keep the body from losing electric charge, we must haveKEmax = hν - W = Vstop qe where qe is the magnitude of the electric charge... If the derived formula is correct, the Vstop when plotted as a function of the frequency of the incident light, should yield a straight line whose slope should be independent of the nature of the substance illuminated.
Einstein's 1905 explanation of the photoelectric effect using quanta of light, later called photons, was the major work cited in his award of the 1921 Nobel Prize for Physics. (Einstein's proposal on relativity was considered too speculative for a Nobel.) The American, Robert A. Millikan (1868-1953) painstakingly developed procedures to avoid effects of surface corrosion and other contaminates to confirm Einstein's prediction that the photoelectric effect from reactive metals all give the same straight line slope equal to Planck's constant, h. For this he was awarded the 1923 Nobel Prize for Physics.
Conceptually the photoelectric effect is also reversible. In practice electrons can be accelerated by high voltage to strike the surface of a metal where photons of light are emitted. If thousands of Volts potential is used to accelerate the electrons, the emitted light will be equally high energy X-rays. In 1923 the American Arthur H. Compton (1892-1962) scattered X-rays off a block of graphite finding that the X-rays behaved as quantum particles, transferring a portion of their momentum and energy to the carbon atoms so that the scattered X-rays had increased wavelengths, λ, (reduced frequencies, ν, and reduced energy, E = hν) depending on the angle of scattering. For this confirmation of the quantum theory he received the 1927 Nobel Prize for Physics.
So there is this paradox that light behaves both as continuous waves and as discontinuous particle-like quantum bundles of energy. If that were not strange enough, in 1924 Louis-Victor Pierre Raymond de Broglie (1892-1987 Nobel photo at right) writing for his doctoral thesis at the Sorbonne in Paris suggested based on the striking symmetry in nature that (1) if the universe is compose of exclusively light and matter and (2) light has the dual nature of waves and particles, perhaps matter also has a dual nature. Assuming that the relationship for matter is the same as for light, a particle's wavelength, λ, is given by
His professors were preparing to refuse granting him a degree for an obviously ridiculous proposal when Einstein visited, heard of deBroglie's weird proposal, and subsequently wrote a paper considering the idea. Meanwhile C.J. Davisson and L.H. Germer in the United States began in 1923 a study of collisions of electron beams with crystals that gave a surprise diffraction pattern that they only later discovered could be explained by deBroglie's proposal. The results were confirmed in 1927 by G.P. Thomson who directed a beam of electrons through a thin gold foil. In both cases the electron particles showed the diffraction pattern of waves with wavelength, λ, predicted by deBroglie. deBroglie was awarded the 1929 Nobel Prize for Physics.
While the wave-particle duality of matter and light may seem a bit weird compared to our daily perceptions of the world, there are profound implications. Waves don't occupy particular points in space but spread over regions. For low momentum (perhaps due to low mass) particles their position is fuzzy because their wave does not have a precise location. Max Born (1882-1969) was the first to suggest that if Ψ represents a mathematical wave function describing a particle, squaring the function, Ψ2, gives a positive function that serves as the probability of where the particle is located. Werner Heisenberg (1901-1976) extended this further noting that the wave nature of light and matter limits what we can know. Uncertainty in location Δx and uncertainty in momentum, ΔP are as least as great as
This as we shall see not only limits what can be known, but also provides a realm in which violations in our laws of physics are permitted: Objects can be multiple places at once and single, lone particles can pass simultaneously through two slits causing interference patterns. And in the realm of elementary particles, even stranger things become possible!
next Experiment
to ie-Physics menu
to site menu
