![]()
![]()
Galileo discovered four moons orbiting Jupiter and challenged others to make careful measurements of their periods. Tables of their movements were developed by Borelli (1665) and Cassini (1668). These tables were based mainly on observations near the time when Jupiter was in opposition, (when Jupiter is opposite the Sun) because this is when Jupiter appears highest and brightest in the night sky. The orbital periods of Jupiter's four moons were found to be 1.769 days, 3.551 days, 7.155 days, and 16.689 days. These seemed to be very constant and predictable, just like all other heavenly motions. Based on these figures it was possible to predict within minutes the times of eclipses and passages (the passings behind and in front of Jupiter) that would occur in future observations.
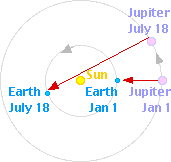
Knowing when these passages should occur, people began to make observations at times when measurements were more difficult such as when Jupiter was nearly in conjunction (together in the sky) with the Sun, but when it was just possible to observe Jupiter just after sunset or before daybreak. But the eclipses and passages of Jupiter's moons at conjunction, which had be predicted so precisely when Jupiter was in opposition, were consistently later than their predicted occurrence. All the four moons seemed to be late by the same amount. The early astronomers actually measured up to 22 minutes late, but more recent measurements have shown that the lateness
is slightly less than 17 minutes.
At the subsequent oppositions six months later, all the moons were found to be back on their predicted schedule! While mulling over this data in 1675 on a visit to Paris, the Danish astronomer Ole Roemer (1644-1710) thought of an explanation based on: sight is not instantaneous.
If light travels at a finite speed, when we see distant things we are really seeing how they were at some time in the past. The further away from an object, the greater the time delay in our viewing. Applying this hypothesis to the observations of Jupiter's moons, Roemer realized that when Jupiter was in conjunction with the Sun, light from Jupiter and it's moons had to travel the extra distance equal the diameter of the Earth's orbit. Using this distance of two radii of the Earth's orbit (that is, two Astronomical Units) and the time of delay, Dutch Christiaan Huygens (1629-1695) made the first reasonable calculation of the speed of light (about 1AU / 8.5 minutes = 3.0 x 108 m/sec).
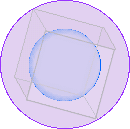 Other European astronomers also made important measurements and calculations. Johann Kepler, Keppler, Khepler, Kheppler, or Keplerus (his spellings!) was conceived May 16, A.D. 1571 at 4:37 A.M. and born December 27 at 2:30 P.M. (according to him) in Weil der Stadt (Weil-the-town) in southwest Germany with the handicaps of poverty. (In 1630 he left his own family penniless, dying while journeying alone in search of money owed him.) His father had abandoned the family, his brother bullied him, his epileptic aunt was burned as a witch and his mother later almost met the same fate. But Kepler received a free education because the new Lutheran church believed everyone needed to study the Bible for themselves. Bright enough to receive advanced education designed to produce church leaders, Kepler could only find a job teaching mathematics, astronomy, and astrology. One day in class while drawing circles just inside and outside of a triangle, he realized the geometry fixing the ratio between the two circles could be the clue to understanding the spacing of the planets. Perhaps the spacings between the 6 planets of Copernicus (Ptolemy counted 7 including the Moon and Sun) was established by the 5 perfect flat sided solids known to Pythagoras. Kepler's subsequent laborious effort found the sizes of the planet orbits DID match within experimental error. Inside the orbit sphere of Saturn, Kepler calculated the largest cube that would fit. He next calculated the largest sphere for Jupiter's orbit that would fit inside the cube then determined the ratio between the two orbits. (Diagram above) Saturn was the furthest away, the slowest moving, and thus the most difficult to measure So Kepler found a 10% error acceptable. The close or perfect fit of the other planets convinced Kepler that the world is indeed Copernican. (Explaining the spacings of Ptolemy's 7 planets would require discovery of a sixth perfect solid.) Publication of his Mysterium Cosmographicum in 1597 explaining the spacings of the planets established Kepler's reputation as a leading astronomer. (Shown at right from Kepler's book is the arrangement of inner planets and larger below is the arrangement of outer planets.)
Other European astronomers also made important measurements and calculations. Johann Kepler, Keppler, Khepler, Kheppler, or Keplerus (his spellings!) was conceived May 16, A.D. 1571 at 4:37 A.M. and born December 27 at 2:30 P.M. (according to him) in Weil der Stadt (Weil-the-town) in southwest Germany with the handicaps of poverty. (In 1630 he left his own family penniless, dying while journeying alone in search of money owed him.) His father had abandoned the family, his brother bullied him, his epileptic aunt was burned as a witch and his mother later almost met the same fate. But Kepler received a free education because the new Lutheran church believed everyone needed to study the Bible for themselves. Bright enough to receive advanced education designed to produce church leaders, Kepler could only find a job teaching mathematics, astronomy, and astrology. One day in class while drawing circles just inside and outside of a triangle, he realized the geometry fixing the ratio between the two circles could be the clue to understanding the spacing of the planets. Perhaps the spacings between the 6 planets of Copernicus (Ptolemy counted 7 including the Moon and Sun) was established by the 5 perfect flat sided solids known to Pythagoras. Kepler's subsequent laborious effort found the sizes of the planet orbits DID match within experimental error. Inside the orbit sphere of Saturn, Kepler calculated the largest cube that would fit. He next calculated the largest sphere for Jupiter's orbit that would fit inside the cube then determined the ratio between the two orbits. (Diagram above) Saturn was the furthest away, the slowest moving, and thus the most difficult to measure So Kepler found a 10% error acceptable. The close or perfect fit of the other planets convinced Kepler that the world is indeed Copernican. (Explaining the spacings of Ptolemy's 7 planets would require discovery of a sixth perfect solid.) Publication of his Mysterium Cosmographicum in 1597 explaining the spacings of the planets established Kepler's reputation as a leading astronomer. (Shown at right from Kepler's book is the arrangement of inner planets and larger below is the arrangement of outer planets.)
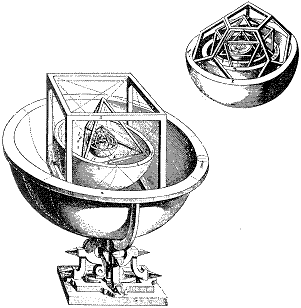
| Planet | Solid spacer | Copernican spacing | Kepler's model | % error | Saturn |
| cube | 0.635 | 0.577 | 10% | |
| Jupiter | ||||
| tetrahedron | 0.333 | 0.333 | 0%!!! | |
| Mars | ||||
| dodecahedron | 0.757 | 0.795 | 5% | |
| Earth | ||||
| icosahedron | 0.795 | 0.795 | 0%!!! | |
| Venus | ||||
| octahedron | 0.702 | 0.707 | 3% | |
| Mercury | ||||
Aristocrat Tycho Brahe (1546-1607) lived a luxurious life after his father died saving the king of Denmark from drownding in a mote. While at university he noted a predicted conjunction was days late and decided more accurate predictions would require more accurate observations and measurements. So with sinecures from the King, he built the world's largest observing tools which he calibrated to the limits perceivable by human vision. One of his early accomplishments was to observe a nova, a star never before seen that seemed to appear in the presumably unchanging sky. After the king's death and the royal financing ended, Brahe obtained employment as the royal mathematician and astronomer to the last Holy Roman Emperor in Prague. Brahe hoped to establish a compromise system in which the Sun and Moon orbited the Earth, while all other planets orbited the Sun. Realizing he needed an assistant for the tedious calculations, he hired Kepler.

Kepler was assigned to calculate the orbit of Mars since Brahe found it most poorly fit predictions. Kepler, claiming he could do the problem in 8 days, took 8 years. After a year, Brahe died, perhaps due to over indulgence, Kepler stole Brahe's journals, and himself obtained the job as royal mathematician and astronomer. Brahe had made 10 precise sightings of Mars and Kepler made two more. These sightings did not fit the Copernican system, nor did adding an equant help. In frustration, Kepler plotted what he called a clean orbit
then noted Mars changes speed. Drawing out rays from the Sun every 1°, Kepler noticed that the radius of Mars sweeps out equal areas in equal times. It moves more rapidly when closer to the sun, then slower when further away. After rejecting several kinds of orbits that closely fit the sightings because he had confidence in the precision and accuracy of Brahe's measurements, Kepler found the path of Mars was actually an ellipse with the Sun at one focus! The universal belief was false that the perfect heavens required circular motion.
Accurately observing the position of an object like Mars in the sky only provides direction but not its distance. This information alone could not establish the location of Mars. Since ancient times everyone presumed the stars were fixed to the celestial sphere. Copernicus had claimed that the celestial sphere was a great distance away. But Mars, like all planets, was thought to be considerably closer and continuously moving.
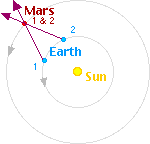
According to the Copernican system, the Earth is moving in a circular orbit providing moving vantage points. So a second observation at a different time provides a different view of Mars. But Mars is also moving, making a second random viewing of no value for determining its location. Ancient astronomers had noted that Mars falls behind the stars, moving even more slowly than the Sun so that it is passed by the Sun 37 times in 79 years. But according to Copernicus, IF the Earth and Mars are orbiting the central Sun at the same rate, like cars travelling the same speed together around a speedway, Mars would NEVER APPEAR to be passed by the Sun. So during one Earth orbit taking one year, Mars makes a hidden common orbit around the Sun. But Mars is actually slower, being passed by the Earth 37 times in 79 years. So according to Copernicus, Mars actually completes only 79 - 37 = 42 orbits in 79 years. If this is correct, Mars will complete one orbit and be back to the same actual location in the sky every 1.88 years = 687 days. If our second observation of Mars is 687 days after the first, we will have two perspectives of Mars in the same location allowing us to determine one point on Mars' orbit using parallax.
In this experiment we wish to make key observations about Mars' direction in the sky, then use those measurements to plot the famous orbit of Mars and determine its parameters.
 Below is a portion of a wide angle photograph of the March 21, 1931 night sky taken with a wide angle camera (shown at right) at the Harvard College Observatory. A search was made of the Observatory's vast collection of routinely made photographic plates for pairs of photographs showing Mars 687 days apart. Mars is back at the same location but the Earth is 43 days shy of completing two orbits in that time period. So knowing where the Earth is on each date and knowing the direction in the sky towards Mar provides two perspectives allowing us to use parallax to plot the location of Mars. On this and the next two screens are 8 pairs of such sky photographs and accompany sky maps of those regions of the sky.
Below is a portion of a wide angle photograph of the March 21, 1931 night sky taken with a wide angle camera (shown at right) at the Harvard College Observatory. A search was made of the Observatory's vast collection of routinely made photographic plates for pairs of photographs showing Mars 687 days apart. Mars is back at the same location but the Earth is 43 days shy of completing two orbits in that time period. So knowing where the Earth is on each date and knowing the direction in the sky towards Mar provides two perspectives allowing us to use parallax to plot the location of Mars. On this and the next two screens are 8 pairs of such sky photographs and accompany sky maps of those regions of the sky.

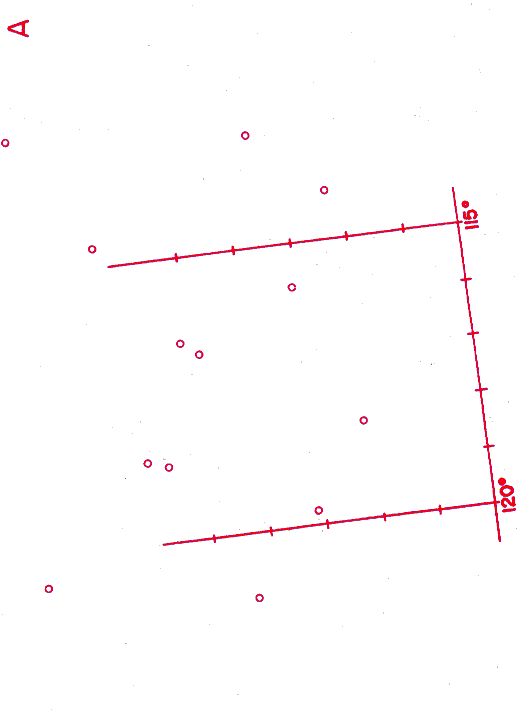
With these 16 measurements, we are now ready to plot the orbit of Mars and analyze its shape.
| Plate | Date | Longitude | Plate | Date | Longitude | |
| A | March 21, 1931 | 0° | B | February 5, 1933 | 316° | |
| C | April 20, 1933 | 29° | D | March 8, 1935 | 347° | |
| E | May 26, 1935 | 65° | F | April 12, 1937 | 21° | |
| G | September 26, 1939 | 184° | H | August 4, 1941 | 131° | |
| I | November 22, 1941 | 239° | J | October 11, 1943 | 198° | |
| K | January 21, 1944 | 300° | L | December 9, 1945 | 255° | |
| M | March 19, 1946 | 358° | N | February 3, 1948 | 314° | |
| O | April 4, 1948 | 13° | P | February 21, 1950 | 332° |
empty focusan equal distance from the circle center but opposite the Sun.
![]()
to next screen of photographs and maps
to next experiment
to ie-Physics menu
to site menu