Music predates both language and recorded history. But understanding of sound as waves came much later. Pythagoras (fl ~522 B.C. ←statue at left) spoke of strings of varying length producing different notes when plucked. The Pythagoreans were probably not the first to discover that uniform strings with lengths in the ratio of 12:9:8:6 produce harmonious sounds. Those ratios we call the octive, fifth and fourth (and the Greeks called diapasõn, diapente, and diatessarõn). There is very little to suggest they had any conception of sound waves. But their interest in numbers and their emphasis on both sensual and eternal harmonies laid the framework for later understanding of sound waves which probably grew slowly over centuries.
Aristotle (b384B.C. d322B.C. statue at left→) extended the Pythagorean harmonic ratios for plucked strings to reed pipes. But he confused the frequency of vibration with the speed of transmission, considering a higher pitched sound to be one which travelled faster. Aristotle did note the higher pitch of an echo but an explanation was not available until Lord Rayleigh proposed a theory in 1873. A contemporary of Aristotle at the Lyeum, Aristoxenos, wrote a book, Elements of Harmony, covering topics of pitch, notes, intervals, scales, keys, modulation, and melody including a much elaborated theory of musical intervals which was more influential on Byzantine music.
Waves such as those which cross the surfaces of bodies of water existed long before there were humans. Some animals may also have taken an interest in such waves before humans. There is no historical record of when waves because a topic of interest to humans, but it likely was long before either language or oral history were launched. People probably threw pebbles into water and observed many of the properties of waves very early. By Aristotle's time, many of the phenomena that we now attribute as wave effects were known, but few were explained by any theory of waves. Only later when there were efforts to understand other phenomena such as sound and earthquakes was there thought they might be similar to more familiar water waves.
propertiesThe series of photographs to the right ⇒ show one long coiled slinky spring which is attached firmly to the wall on the right. In the top image a transverse wave has been generated by a rapid jerk upwards and back down. In successive images down the screen, the wave moves to the right → then reflects off the wall back to the left ←. Note the wave was primarily above the original position before hitting the wall, and is reflected below afterwards. (These are similar to a side view of waves traveling on the surface of water.)
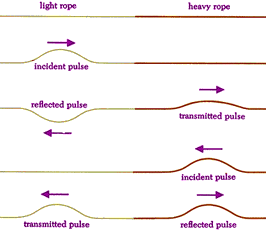But this isn't always the case. Reflection also occurs at a boundary when part of a wave passes from one medium to another. On the left ⇐ a light weight rope is connected to a heavier rope. Note what happens when an incident wave approaches going from the light rope to heavy ropes → as opposed to going from heavy rope to light rope ←.
Note that the reflected wave maintains the same shape and speed of the incident wave although the size may be diminished.
refraction
The top photograph at right→ is an overhead view looking down upon a series of water waves moving from left to right⇒ at a constant frequency, ν. When they reach the barrier, the waves above the barrier in the photograph continue with the same wavelength, λ. Below the barrier in the photograph, the waves travel in shallow water. Note the speed of the waves is slower in shallow water so that the wavelength, λ is shorter.
In the bottom photograph at right→, a series of constant frequency waves is moving initially from left to right⇒. A wedge shaped region of shallow water occupies the lower portion of the photograph. Note when the the waves encounter shallow water, they travel more slowly while the portion of the waves in deep water maintain their previous speed and wavelength. (Note the difference in length of wavelength arrows.) As a result of encountering the shallows at a diagonal, the portion of the waves which have travelled longer in the shallows lag further behind, effectively resulting in the waves changing direction. This process is called refraction. It is used to re-focus light in eye glasses.
In the top photograph at left←, a series of constant frequency waves is moving from down the screen↓. When the waves encounter a barrier on the right side of the photograph, the waves are reflected effectively leaving smooth flat water below the barrier. However waves that continue unimpeded left off the end of the barrier, spread out so that a portion of each wave curves around behind (below) the barrier. This curving behind a barrier is called diffraction. The middle photograph shows the diffraction which occurs when waves pass through a small opening in the barrier. We commonly hear by diffraction sounds from another room which have expanded after passing through a doorway.
The bottom photograph shows what happens when a series of constant frequency waves is moving from down the screen↓ pass through two nearby openings in a barrier. Waves diffract after passing through each opening. But when the spreading waves from one opening cross the waves from the other opening, there is interference. Unlike common objects which only allow one to occupy a space at a time, multiple waves can occupy the same space. This allows waves traveling different directions to pass through each other. Apparent interference results because of superposition where at any location the height of the wave is the sum of all the waves at that location. Where a wave crest meets a wave trough, the waves at least partially subtract resulting in less wave amplitude. Where multiple crests meet or multiple troughs meet, the amplitudes combine to make a larger crest or deeper trough. (Notice this in the sequence of diagrams below.) When the difference in distance travelled from the opening in the barrier is a partial wavelength, there are wedge shaped regions where waves deconstructively superimpose to produce nodes with only small if any waves. (These nodes may be easier to locate if you squint at the bottom photograph.) Other wedge shaped regions are distances which differ in distance from the openings by a whole number of wavelengths, resulting in the waves constructively superimposing creating larger waves.
Jean Baptiste Joseph Fourier (b1768, d1830 ←portrait at left) rose from orphaned son of a tailor to the French imposed governor of Lower Egypt. In his 1822 Théorie analytique de la chaleur, he claimed that any function of a variable, whether continuous or discontinuous, can be expanded in a series of sine curves. Such Fourier analysis to determining the individual sine wave components of a complex signal is widely uses from eliminating the hum caused by alternating electric current to JPEG compression used to aid transmission of pictures via the Internet. (In a 1827 essay Fourier proposed that gases in the atmosphere might increase the surface temperature of the Earth, an early proposal of the greenhouse effect. He established the concept of planetary energy balance and proposed that planets also lose energy by what he called dark heat 25 years before the discovery of infrared light.)
Wave patterns can also be rapidly sampled to determine the wave amplitudes at very closely spaced time intervals. Each can be coded in a numerical digit allowing the information can be accurately and economically transmitted so that wave function can be reconstructed at another location or time. Modern communication of music and other sounds nearly universally uses these digitized waves.
Why are most of these waves curved? Why are some crossing? How many different wave phenomena are visible? Can you identify all of them?
Can you tell the direction of motion of all the waves? Can you explain what role the cement wall played in the crossed waves in the last photograph? Can you explain why a wave breaks when it get into shallow water?
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
to next Experiment
to ie-Physics menu
to site menu
