ie-Physics

Summary and Practice Applications of Basic Physics Skills

© by William Dietsch 1998

• Vectors are quantities, which require magnitude and direction for their complete description.
Examples of vectors are force, acceleration, and velocity, among many others. Scalar quantities only require magnitude.
Temperature, mass, and speed are examples of scalar quantities.

• Vectors must be added and subtracted by means of geometric methods.  Linear vectors (acting on the same line) may be added algebraically by use of positive and negative signs, which indicate direction.  Using + for up and -for down is a common example of this.

• Two dimensional vector analyses is accomplished by the use of geometric methods.

• Graphic analysis uses scale drawings to find the sum or difference of two or more vector quantities.

• The trigonometry of right and scalene triangles may be used to add two vectors in the same plane (coplanar vectors).

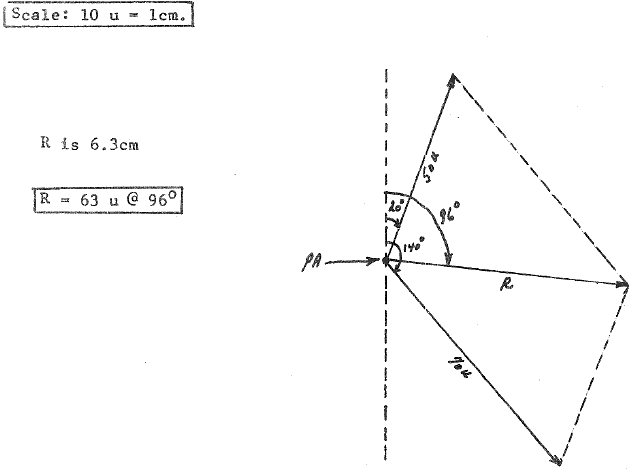
Parallelogram method for vector addition

1. Choose an appropriate scale (e.g., 10 units [U] = 1 cm).
2. Draw a vertical reference line. (For reference orientation and angle measure)
3. Place a point of application (PA) on the reference line.
4. Draw the first component to scale with its tail at the point of application.
5. Draw the second component to scale with its tail at the point of application.
6. Construct a parallelogram with the two components as adjacent sides.
7. Draw the resultant as the diagonal of the parallelogram pointing away from the PA.
8. Measure the length of the resultant line and use the scale to determine the magnitude.
9. Determine the direction of the resultant using the vertical reference line and the PA at the vertex of the angle

Example:

Polygon :method for vector addition

1. Choose an appropriate scale (e.g., 10 units [U] = 1 cm).
2. Draw a vertical reference line. (For reference orientation and angle measure)
3. Place a point of application (PA) on the reference line.
4. Draw the first component vector to scale with its tail at the point of application.
5. Draw a new vertical reference line at the head of the first vector arrow.
6. Draw the second component vector arrow with it's tail at the head of the first.
7. Draw a new vertical reference line at the head of the second vector arrow.
8. Draw the third component vector arrow at the head of the second.
9. Continue drawing in the rest of the vector arrows repeating the procedure above.
10. The resultant is the arrow with it's tail at the PA and its head at the head of the last component arrow.

Example:

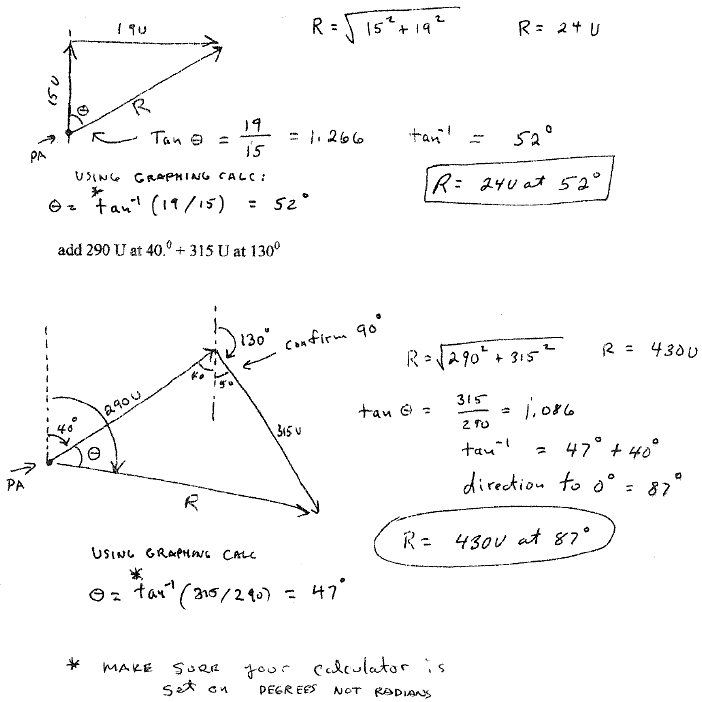
Vector addition using trigonometry I

1. Confirm that the two vectors are at right angles to each other (the difference is 90°)
2. Sketch the solution to the problem using the Polygon method (head to tail).
3. Compute the magnitude of R using the Pythagorean theorem.
4. Compute the value of Θ using the tangent function.  Note: Θ is the angle with the PA at it's vertex.
5. State the direction of the resultant relative to 0°.

Examples:

Vector addition using trigonometry II

1. Sketch the solution using the polygon method (head to tail).
2. Find α (the angle with the components as sides).
3. Compute the magnitude of R using the law of Cosines.
4. Compute the value of Θ (angle with the PA at the vertex) using the law of Sines.
5. State the direction of the resultant relative to 0°.
6. See advice below if using a graphing calculator to find the solutions.

General Case:

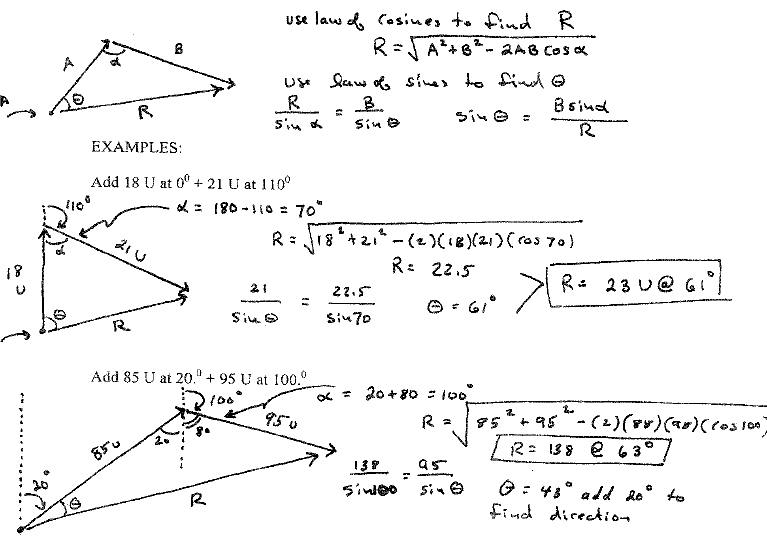
Solving for R using graphing type calculators:

Example 1

R = √((18² + 21²)-(2*18*21 *cos70)) ENTER This will find the magnitude of R.
Θ = sin^-1 (21*sin70/22.5) ENTER   This will find the value of Θ.