Experiment C1 Described what we current understand about how the Hydrogen and some of the Helium of the universe was synthesized and the nature of the evidence that has led us to that understanding. Experiment C2 explain how additional Helium has been assembled at high temperatures in the cores of main sequence stars such as our Sun. While we can duplicate that process in Hydrogen bombs and in particle accelerators, confirming evidence also comes from radiation emitted from the Sun. However main sequence stars are not hot enough to force together Helium to make the heavier atoms found in the rest of the elements found here on Earth.
Most of the other atoms composing the earth were synthesized in a less abundant type of star where the temperatures are far hotter. As mentioned in the previous web page, the pressure created by the Hydrogen fusion occurring in the core of a main sequence star balances the gravity attracting the matter tighter together. This balance often lasts billions of years depending on the mass of the star. Larger stars have stronger gravitational attraction resulting in hotter cores. As a result, larger stars fuse Hydrogen in their cores to Helium faster resulting in briefer times as main sequence stars. Astronomers have calculated that our sun has been a main sequence star for about 5 billion years and is about half way through that process.
Eventually much of the Hydrogen in the core of a main sequence star will be fused to Helium resulting in less pressure which in turn will allow gravity to resume compressing the core of the star. As the core is further compressed and heated, eventually new types of fusion can occur creating elements larger than Helium.
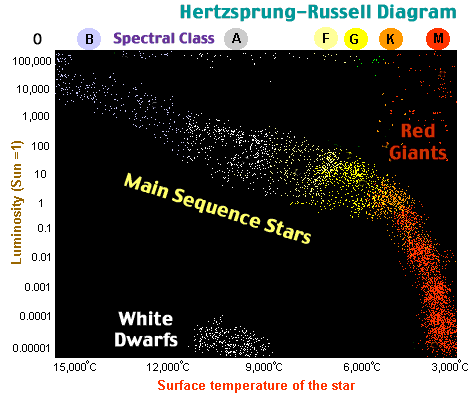The matter in the center of stars is very dense preventing much mixing. While the core of a main sequence star becomes depleted in Hydrogen, the surrounding layers of the star still contain massive amounts of Hydrogen which was never hot enough to fuse. Now as the star's core is further compressed, that surrounding layer of Hydrogen is finally compressed and heated enough to begin fusing to Helium. Strangely, the rate of Hydrogen fusion is now greater than occurred during the main sequence stage. As a result of the greatly increased energy output, the star puffs up the outer layers of Hydrogen. When the Sun becomes such a star it will swell larger than the earth's orbit! The outermost surface will be so far from the fusion that it will be somewhat cooler that the yellow glowing surface of main sequence stars. Such a bloated star will appear only dull red, earning the classification as a red giant star.
When the core of a red giant is compressed enough to reach a density of about 104 g/cm3 and a temperature of 108 K, atoms collide with sufficient speed for elements larger than Hydrogen to fuse. Of the several fusion reactions possible, the reaction called Helium burning occurs most commonly.
This generates enough energy to again stop the gravitational collapse. Notice that this process skips synthesis of the intervening elements Lithium (Li), Beryllium (Be), and Boron (B), which is consistent with their relatively small abundance in the universe. As mentioned in Experiment C2, at the core temperature of a red giant, these elements are unstable and have very short half lives. The nearly simultaneous fusion of three atoms may seem improbable however at the extreme density in the core of a red giant where Helium nuclei are very close together, Helium burning is the dominate reaction.
At this temperature and pressure additional fusion can occur with Helium and Hydrogen as exemplified by
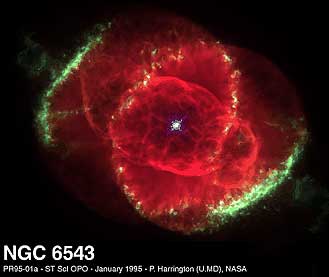
These two processes for the most part synthesizes in red giant stars elements from Carbon (#6) to Neon (#10). If the star has only several times the mass of the Sun, it will expel considerable amount of its mass. Eventually when the fusion fuel is exhausted and the mass diminishes to less that 1.4 times the Sun's mass, the star will cool to what is called a white dwarf star. Because it is no longer producing energy, its intensity will be faint, dimming over a very long time as it very slowly cools. White dwarfs are very small, for example one with mass is approximately equal that of the Sun will have shrunk to the size of the earth. For some time it may be surrounded by the ejected cloud of gases, still glowing, as in the Cat's Eye Nebula (shown to right. Because it is still much brighter than the glowing gases, the size of the central white dwarf has been greatly exaggerated in this Hubble photo due to overexposure).
If a red giant star has a mass greater than 8 times that of the Sun, it's core can slowly collapse creating even hotter conditions of about 109 K and a density of about 106 g/cm3. At these conditions two additional kinds of fusion are initiated as the other kinds continue in layers further from the core. What is called Carbon burning involves two atoms of roughly the size of Carbon.
For a star with 25 solar masses, these processes may continue for 600 years synthesizing elements such as 2412Mg, 2814Si and 3216S. At temperatures approaching 3 x 109 K, these new heavier elements can also undergo fusion with lighter elements such as Helium in a process called Silicon burning.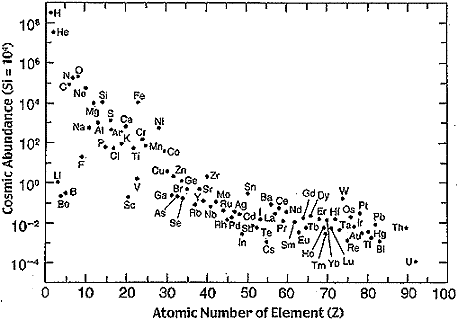
These processes preferentially produce elements with atomic masses of 32, 36, 40, 44, 48, 52, 56 which are more abundant in the universe than similarly sized elements. These processes can synthesize elements up to Iron (5626Fe) while also releasing energy. However synthesis of elements larger than Iron are endothermic and absorb rather than release energy. As a result only small amounts of heavy elements are produced in red giant stars. The slow synthesis of elements heavier than Iron is therefore sometime called the s-process. It is believed to synthesize elements up to 83Bi after which the decay rate exceeds the rate of synthesis.
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
to next experiment
to Cosmology Chemistry menu
to ie-Chemistry menu
to site menu
