ie-Physics

Experiment IV-7

While William Gilbert summarized the properties of magnetics and electricity in 1600, he did not believe that electric bodies could repel.  But in 1646 Sir Thomas Browne published an account of electrical repulsion.  A century later the repulsion of two negative charges proved difficult for Benjamin Franklin's proposal that only one kind of fluid exists.  How could two bodies experience electrical repulsion if Franklin claimed they were deficient of electric fluid?

About 1775 Franklin noted a small cork hanging outside an electrically charged metal can was strongly attracted, but when lowered by a thread inside the can, the cork experienced no force.  Franklin had difficulty understanding why the cork did not experience a force especially when located inside but very near the charged metal can.  The protestant clergyman Joseph Priestley (1733-1804 at left), whose destiny was changed by meeting Franklin in London, repeated the experiment.  Recalling that Newton had written that because of the inverse square force law there would be no gravitational force inside a hollow planet, Priestly surmised by analogy that a similar inverse square law must apply for electric force.  The French physicist Charles Augustin de Coulomb (1736-1806 at right) invented a delicate torsion balance and used it to provide experimental verification of such an inverse square law.

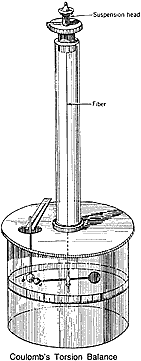
Coulomb's balance (shown here) used a pair of spheres suspended by a long, easily twisted fiber inside a shielded case.  When another charged sphere was nearby, the fiber supporting the spheres was slightly twisted.  To vary the amount of charge, an identical uncharged sphere was touched to one of the charged spheres.  The electric fluid was shared equally between the two spheres, resulting in half the original charge on each sphere.

Today scientists often need to use equipment beyond their personal ability to build or purchase.  Research institutions around the world used government and other grant monies to build such equipment.  The institutions either host scientists selected to perform proposed experiments, or the institution support staff conducts the proposed experiment and supplies the results to the scientists who proposed the research.  It is not so much that the expense is too great or that equipment such as Coulomb created is too difficult to make.  Rather perfecting the apparatus and gathering usable data requires great patience and care.  Over several decades, students in the author's classes have experienced much difficulty gathering suitable data.  Therefore data from more successful attempts has been gathered and provided in the table below:

Experiment

Equipment needed:

calculator

graph paper

data from equipment (provided below)

Procedure:

1. Somewhat different apparatus was setup as follows:
   1. The entire apparatus was surrounded by a cardboard box to block any air drafts.
   2. A small, light weight, electrically charged sphere was hung from two long threads so it could easily swing in one direction but not in a perpendicular direction.
   3. A second, identical sphere mounted on a movable insulating support was touched to the first so they shared equal electric charge.
   4. A mirror with an attached metric scale was placed below the spheres so that parallax could be minimized when viewed from above.
   5. The mounted sphere was moved various distanced from the swinging sphere and the mean (average) deflection of the swinging sphere measured.  For small angles of deflection, the amount of deflection is proportional to the repulsive force.  (For example, three times as much electrical repulsion would cause the swinging sphere to be deflected three times as far from hanging straight down.)
2. Calculate the reciprocal of the distance of separation, 1 / d.
3. Calculate the square of this reciprocal of separation distance.
4. Graph the value of the electrical force verses the reciprocal of the square of the separation distance to determine if there is a proportion.

5. If a graph has a straight line passing through the origin, the property of the vertical axis is equal to the property on the horizontal axis times a constant.  What equation fits the relationship between the electrical force and the separation distance between the electrically charged bodies?
6. The electrical charge on the movable sphere is reduced in half by touching an identical but electrically uncharged sphere.  When the separation distance to the swinging sphere with unchanged charge is 1.0 cm, the deflection is only 3.3 cm.  Is the electrical force proportional to this charge?
7. We don't need experimental information for variations in the swinging electrical charge.  We can appeal to symmetry.  How to the electrical charges know which is agent and which is victim?  What we found true for one electric charge in step 6 must be true for the other electric charge as well.  What equation correctly gives the relation between electrical force, the distance of separation, and the magnitude of each electric charge?

Finally, record your procedures, measurements, and findings in your journal.  If you need course credit, use your observations recorded in your journal to construct a formal report