In Experiment IV-1 you probably found that light reflects on a flat surface with the angle of reflection equal to the angle of incidence. This might be explained by thinking of light as composed of particles or corpuscles that conserve momentum as they bounce. A non-spinning billiard ball, basketball, or soccer ball illustrates similar behavior.
But alternatively, the reflection of light might also be explained by thinking light as a series of waves which are also know to reflect off of flat barriers with their angle of reflection equal the angle of incidence.
In Experiment IV-2 you probably found that light travelling from air into water refracts, changing direction, heading in a direction closer to perpendicular compared to the boundary between the air and water. This could be explained by a wave slowing down as it crossed the boundary. If a light wave encountered the boundary at an acute angle, the portion of the wave already in the water would travel more slowly while the portion of the wave not yet to the boundary would maintain its speed until it too encountered the boundary.
Or if you prefer, this refraction of light entering water might be thought of as light particles or corpuscles being attracted by the water so that they gained increased momentum perpendicular to the boundary as they entered the water.
Notice that we have two rival explanations for the behavior of light. Light can be either thought of as particles or corpuscles which travel from the source to the observer, or as wave-like disturbances in an otherwise relatively stationary medium. In the case of waves, only the disturbance travels from source to observer, not the medium. Both theories are equally able to explain the reflection and refraction of light, but they do make a critical distinction explaining refraction. The wave theory predicts light SLOWS when entering water from air, while the particle theory predicts light GOES FASTER in water than in air.
The Italian Galileo Galilei (1564-1642, shown at left) proposed one of the first efforts to measure what he believed would be a finite speed of light. He proposed stationing two experimenters on distant hills at night with lanterns and a box to cover each. When ready the first would uncover the first lantern allowing light to emerge. When the second experimenter first saw the light from the first lantern, she or he would immediately uncover the second lantern allowing light to start a return journey. The first experimenter would notice how long it took between the emergence of the first lantern's light until the arrival of light from the second lantern. The speed would be the round trip distance divided by the elapsed time: s = d / t. While conceptually sound, the time observed was short compared to the inaccuracy contributed by human reaction time.
In Holland Christiaan Huygens (1629-1695, shown at right) used data collected by Danish astronomer Ole Roemer (1644-1710) on the variations in the period of Io, Jupiter's moon, to determine the speed of light. Roemer had noted that the eclipses and passages of Jupiter's moons at conjunction, which had be predicted so precisely when Jupiter was in opposition, were consistently later than their predicted occurrence. All the four moons seemed to be late by the same amount, up to 22 minutes. Roemer realized that the time difference was due to differences in distanced between when the earth was closest to Jupiter and furthest from Jupiter. Huygens calculated this difference in distance and then the speed of light (about 1AU / 8.5 minutes ≅ 3 x 108 m/sec).
But the measurement of the speed of light in water was technically much more challenging and not accomplished until much more recently.
Like much of physics, this experiment extends from the wildly impractical of the imagination to the understanding that makes many of our lives better. You may not care about the speed of light in water, but eventually most of us will need glasses to make our vision clear.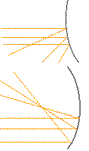
The principles of reflection from flat mirrors apply to curved surfaces as well. Consider each small piece of a curved mirror is essentially flat. But since all pieces are not aligned, different parts of curved mirrors direct light in different directions. A mirror whose edges curve away from you, called a convex mirror, causes parallel light to diverge, seeming to originate from a small source just behind the mirror. Or in reverse, light from a broad panorama gets shrunk to a miniature just behind the mirror. Such mirrors are used to get a broad rear view or a view what's happening all over the store. A mirror with edges curved in towards you, a concaved mirror, like the convex lense in the procedure below, are more complex. Parabolic shaped concaved mirrors are used in spot lights and telescopes.
Likewise the principles of refraction describing the bending of light when entering or leaving transparent solids or liquids with different indexes of refraction are the same for flat and curved boundaries. In the procedure below a convex lense is investigated. However the same procedure may be used with a concaved lense or curved mirrors.
