Waves pervade the universe. We experience sound waves and light waves. Wave mechanics explains atoms and subatomic matter. Loops of waves of energy called strings have been proposed as the essence of everything in the universe.
Waves in deformable (elastic) matter are called mechanical waves. Unlike the transverse motions of objects studied earlier, only the disturbance of the wave moves from one location to another while the displaced matter oscillates around to its equilibrium location. Material can be disturbed by a wave in three distinct directions:
For example in sound, the material can be alternately compressed and rarified in a disturbance that expands outwards from the source. The wave travels the same direction as the disturbance. This is called a longitudinal or compression wave.
On the surface of a liquid (e.g., the ocean) or sheet (e.g., a flag) the material is displaced perpendicular to the surface. For example the surface of the ocean goes up and down as the wave crosses the surface. This is called a transverse wave.
Cohesive materials may be twisted around the axis of the wave travel (e.g., a lawn hose or a wire) with neighboring parts of the material receiving the twist a very short time later. This is called a torsional wave.
View animations of severals waves on Dan Russell's web site at Kettering University. (If using a slow modem, be sure to wait until all three animations load.)
Unlike our common observation that two objects can't occupy the same space, multiple waves can simultaneously occupy the same space. View the top animation on passing waves on Dan Russel's web site.
If a wave strikes a barrier they will reflect. When a continuous series of waves of uniform frequency are reflected from a barrier, the reflected waves will encounter the incoming waves. Wherever a reflected crest meets a similar incoming crest, the two waves will momentarily sum creating a double amplitude wave. Wherever a crest encounters a trough, its opposite, the two waves will cancel creating momentarily a location of near zero amplitude. This process called interference creates a region of standing waves twice the amplitude of the original wave. If the waves are sound waves, the regions of constructive interference will be twice as loud while the canceling regions will be nearly silent. This constructive interference occurs every HALF wavelength. You may wish to view an animation of such standing waves on the Physics Classroom web site and confirm this.
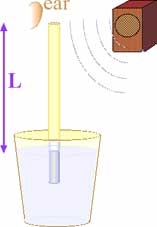
If a continuous sound enters a tube closed on one end, it will reflect at the closed end causing interference. But if the open end is relatively small, a significant amount of reflection will occur there as well. This reflection at the open end can be reduced by flaring the opening as common in many musical instruments. If the tube is just the right length, reflections from both the closed and open ends will result in a resonance of repeated constructive interference with noticeable amplification. But if the tube is any other length, the interference will be destructive. If the sound is a broad buzzing at the closed end created by vibrating lips, only the frequency that is resonant with the length of the tube length will be amplified and produced by the instrument.
In this experiment a single frequency of sound will be produced and the length of the tube modified until it matches that needed to produce resonance and the sound amplified. Gradually changing the tube length will eventually reach another length which amplifies the sound. Doubling the product of the frequency of the sound with the difference in length (which is also the minimum length needed for resonance) will calculate the speed of the sound.
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
to next experiment
to e-Physics menu
to site menu
