The Greeks were the first to propose physical explanations for materials. Anaximenes (of Miletos about 590 to 526 B.C.) claimed that air (pneuma) is the elemental material. Variety of substance is due to thickening or thinning. Empedocles (of Agrigentum 492 to about 400 B.C.) combined aspects of previous Greek proposals about the world's materials. Empedocles suggested that everything consists of four elements: Fire, air, water, and earth, and two forces: love (attraction) and strife (repulsion). (These elements were thought to be related to what we observe in nature, but more pure.)
These ideas were incorporated into alchemy, but over the centuries, air seemed to be the most difficult to handle or understand. Instead of being part of the knowable universe, the cosmos, it was part of the unknowable chaos. Johannes Baptista van Helmont (1577 in Brussels to 1644) coined the word gas to describe those mysterious wild spirits
which could neither be seen nor kept in vessels. van Helmont derived gas
from the Greek word chaos
. (Compare the sounds when spoken.) He did note that gases from different sources seem to have different properties: gas carbonum from burning charcoal, gas sylvester from fermenting wine and spa water, inflammable gas pinque from organic matter, and another poisonous, red gas sylvester from some metals placed in aqua fortis. But alchemists who came after van Helmont utilized a technique of collecting gases by displacing liquids such as water and Mercury from inverted containers. What they learned about the differences between various gases was a major contribution to the eventual over throw of the four element theory and the introduction of a new chemistry by Antoine Lavoisier (Paris, 1743 to 1794) based on a re-definition of element previously proposed by Robert Boyle (1627 in Lismore, Ireland to 1691). That revolution was followed within a few decades by the proposal by John Dalton (of Manchester 1766 to 1844) that particles called atoms and molecules could be used to explain some of the recent chemical discoveries.
But others had discussed the possibility of particles in matter ever since that concept was proposed by Leucippos (perhaps born about 450 B.C. in Miletos). In 1738 Daniel Bernoulli (b1700, d1782) was the first to explain air pressure using moving particles. He proposed considering a container closed by a piston having a weight on it, both supported by the air pressure inside the container: let the cavity contain very minute corpuscles, which are driven hither and thither with a very rapid motion; so that these corpuscles, when they strike against the piston and sustain it by their repeated impacts, form an elastic fluid which will expand of itself if the weight is removed or diminished...
Other scientists generally believed that if a gas contained particles, they stayed more or less stationary by repulsion from each other. After Robert Boyle's 1662 publication of experimental verification of his gas law PV = constant, Isaac Newton (b1643, d1727) showed it could instead be due to an inverse-square repulsive force. In the 1820's John Herapath (b1790, d1868), derived the relationship between pressure and molecular speed, tried to get it published by the Royal Society, but was rejected by the president, Humphry Davy, who pointed out that equating temperature with motion implied that there would be an absolute zero of temperature, an idea Davy thought unreasonable. Herapath used Newton's mechanics: a molecule of mass m and speed v, bouncing off the piston would have a change of momentum of 2mv. This would for a time t create a force F on the piston, 2mv = Ft. The total force on the piston of area A due to a large number of randomly moving molecules would average to the pressure, P = F/A. The total force depends on the frequency of collisions which in turn depends on the number of molecules, n, and the length of the container, L. (The bigger the container, the longer it takes for a molecule to get back for another collision.). So the pressure ends up equaling the average kinetic energy of each molecule, ½mv2 times the number of molecules, divided by the volume (V = L A) of the container: P = n (½mv2) / V
Scottish author C.K.C. MacDonald who was educated partly at Edinburgh describes Scotsmen as a funny breed, obstinate, determined, and often rather reserved (dour), but, when driven to make a comment, usually rather direct in what they have to say. They are suspicious of displays of emotion or exuberance, skeptical, and hard to convince, and in brief, canny. He suspected that the northern climate might have contributed to that common personality. The description fits James Clerk Maxwell (b1831 in Edinburgh, d1879). Grandson to sea Captain Clerk of the East India Company, James gained the Maxwell name when his father, by well-to-do Scottish tradition, added the surname when inheriting that family's estate. It was on that estate the James was raised until sent off to Edinburgh for higher schooling.
From a very young age Maxwell was always asking Show me how it doos.
(sic) or What is the particular go of that?
By age 14 he had advanced beyond just trying to understand particulars to generalizing. He wrote a paper on constructing oval curves which was read to the Royal Society of Edinburgh! (Maxwell generalized the practice of constructing an ellipse by extending a pencil against a loop of string strung around pins at two foci. He proposed generalizing the formula for such curves, for example by looping the string back from the pencil to one of the foci.) As typical of those with first-class minds, Maxwell subsequently contributed to many different phenomena. In his mid-twenties he wrote an essay and later a book on the rings of Saturn proving that they could be neither solid nor liquid.
In 1859 when a number of physicists still had serious doubts about the atomic theory being championed by chemists, Maxwell (←photo at left) wrote a paper on the kinetic theory of gases to the British Association. Various difficulties with the existing theories of heat, such as the caloric theory, prompted a look at the kinetic theory of Bernoulli. Maxwell considered Bernoulli's suggestion that the atoms or molecules in a gas were perfectly elastic particles, obeying Newton's laws, bouncing off each other and the container walls and traveling in straight lines in between collisions. As a result of various collisions, some molecules will be traveling rather slowly, while others rather fast. Maxwell realized that it was impractical to consider each particle separately. Instead, with an understanding of how this microscopic particle motions related to the macroscopic properties, statistics could be used to calculate the bulk properties of a gas. The relevant microscopic information is not knowledge of the position and velocity of every molecule at every instant of time, but the distribution of the molecules in a certain part of the container, and their velocities. The statistical mechanics developed by Maxwell and Boltzmann and the related thermodynamics were achieved while Maxwell also pondered the electrical ideas of Faraday and began to develop his synthesis of electric and magnetic understanding that we call the Maxwell Equations.
In 1863 Austrian Ludwig Boltzmann (b1844, d1906) began a study of physics at the University of Vienna. Boltzmann received his PhD degree in 1866 with a dissertation on kinetic theory of gases. He was supervised by Joseph Stefan who introduced Boltzmann to Maxwell's work.
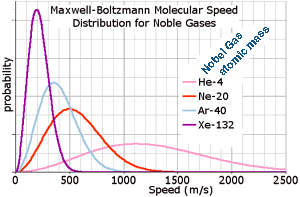The Maxwell-Boltzmann distribution forms the basis of the kinetic theory of gases, and therefore helps explain many fundamental gas properties such as pressure and diffusion. The Maxwell-Boltzmann distribution is usually thought of as the distribution of molecular speeds in a gas. It can be derived using the statistical mechanics created independently by James Clerk Maxwell and Ludwig Boltzmann. The original derivation by Maxwell assumed gases would behave randomly so all three directions would be equivalent, but Boltzmann's later derivation dropped that assumption and instead was based on kinetic theory which has no directional qualities. (Recall that a particle moving at speed v has kinetic energy ½mv2.) The total area under each curve on the graph equals the total number of that kind of molecule so although these don't have the same peak heights, they do have the same number of molecules. Molecules with less mass generally must travel faster to have the same kinetic energy (at the same temperature) as more massive molecules. (So at the same temperature, the Helium atoms are much moving faster on average than Xeon.) If the temperature increases, the position of the maximum shifts to the right for all samples and the peak of the most likely temperature decreases in height, having fewer molecules as their speeds are more widely spread.
Boltzmann (photo at right→) went further, realizing a connection between the statistical analysis of possible states of a large system and a new concept of entropy, a concept that is central to the second law of thermodynamics. Boltzmann proved that the thermodynamic entropy S of a system (at a given energy E) was related to the number W of microscopic states available to it by S = k logW, where k is called Boltzmann's constant, 1.68 x 10-23 J / K. Unlike energy which in a closed system is always conserved, Entropy has a tendency, driven by chance, to increase. The increase over time of entropy of a system as detected by changes in macroscopic variables corresponds to approaching the most probable microscopic arrangements. Boltzmann showed that the numbers of available microscopic states for a given energy are far greater for the macroscopic situation we describe as thermal equilibrium. Consider for example the arrangement of gas molecules in a container. It is much more likely that the gas molecules will be uniformly distributed in then container than say that all the molecules happen to simultaneously be on just one side of the container. So if we arrange for all the molecules to be in the bottom half of a container by using a piston to push them there, then when we remove the piston, the molecules will rapidly tend towards a uniform distribution spread evenly throughout the box. This is because the statistical changes for molecules to be randomly distributed, with a greater entropy value, is much greater than remaining unevenly distributed with a lower entropy value. Boltzmann was then able to establish that for any system large or small in thermal equilibrium at temperature T, the probability of being in a particular state at energy E is proportional to e-E / k T. This is called the Boltzmann distribution.
Boltzmann's analysis of entropy in terms of underlying microscopic configurations was ridiculed by some very powerful German scientists, led by the famous chemist W. Ostwald, who did not believe in atoms! Boltzmann was depressed by these attacks and by his own poor health, and took his own life in 1906. Ostwald got the Nobel prize in 1909. But Boltzmann's analysis turned out correct.
So our observation that heat flows from hot to cold is not a certain process but one of statistics; Molecules at high temperature have only a high probability of moving toward those at low temperature. Maxwell and Boltzmann's approach did not reject the earlier studies of thermodynamics but used a better theory of the basis to explain the observations and experiments.
Perhaps we should go backward in time to consider some concepts about gas behavior and engines which got lost for a while. Nicolas Léonard Sadi Carnot (b1796 in Paris, d1832) was a French artilleryman. Living at a time when steam engines were being introduced, Carnot was struck by the lack of any theory about such engines and the total reliance on empirical procedures for their design. In 1819 he wrote a memoir entitled Réflexions sur la puissance motrice du feu (Reflections on the Motive Power of Heat) but it wasn't accepted for publication until 1824 and then was virtually unread for 25 years. Perhaps because at age 23 he had no prior academic publications to attract attention and only a few copies were printed, the paper was unknown until its discovery by William Thomson resulted in a second edition being published in 1872. Always frail, Carnot was distracted by the Napoleonic wars and revolution of 1830. He developed inflammation of the lungs,
followed by scarlet fever, then when an epidemic of cholera occurred, he died at age 36, only 8 years after publication of his paper, and before he could put his ideas to any practical, noticeable use.
Carnot wrote that if the art of producing motive power from heat were to be elevated to the stature of a science, the whole phenomena must be studied from the most general point of view, without reference to any particular engine, machine, or operating fluid. ...their theory is very little understood, and attempts to improve them are still directed almost by chance. The question has often been raised whether the motive power of heat is unbounded, whether the possible improvements in steam engines have an assignable limit... or whether these improvements may be carried on indefinitely. We propose to submit these questions to a deliberate examination.
Carnot first realized that a fluid must be allowed both to receive and reject heat to allow an operation cycle. For example water is heated to steam, expands and does work, condenses, and is eventually returned to its original conditions where it can be used again. He asked what was the net results of the cycle and noted it was far from what might appear ideal. He suggested that work (W) was produced entirely by letting down heat (Q) from a high temperature source (T1) to a low temperature receiver (T2).
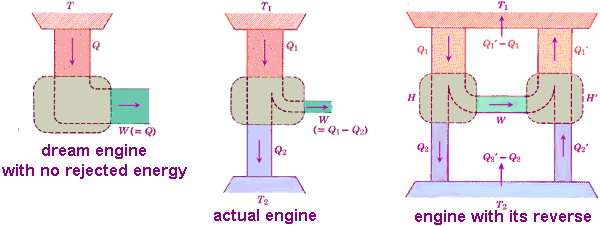
Considering the best possible engine, Carnot proposed a perfect thermodynamic engine, whatever amount of mechanical effect it can derive from a certain thermal agency, if an equal amount be spent in working it backwards, an equal reverse thermal effect will be produced, what we now call a reversible engine. Carnot showed no engine could be more efficient than a reversible engine. He concluded that the maximum efficiency of any heat engine must depend on the temperature at which the heat is both received in the boiler and rejected to some receiver such as the cooled water of the condenser.
Although Carnot expressed doubts about the Caloric theory of heat, his analysis is based on the Caloric theory. J.R. Mayer published in Heilbrom Germany in 1842 a paper proposing that heating water from 0°C to 1°C required the energy of an equal amount of water falling 365 meters. But he received little attention. James Prescott Joule (d1818 near Manchester England, d1889 at right without his later beard→) recognized confusion between physicists and engineers involving the terms work, energy, power and friction. Becoming convinced of the mechanical theory of heat, he conducted a long series of varied experiments which he reported in meetings in 1843, 1845, and 1847. At the latter meeting was William Thomson (another Scotsman b1824, d1907, to become Lord Kelvin in 1892) who came to find fault with Joule's claims, having recently studied a copy of Carnot's memoir based on the Caloric theory. But impressed by the experimental evidence, Thomson introduced himself and established a lifelong friendship. In 1849 Thomson, who had already established a brilliant reputation as a physicist with publication of over two dozen papers, reintroduced Carnot to the world with a paper Carnot's Theory of the Motive Power of Heat with Numerical Results Deduced from Regnault's Experiments on Steam. Using the language of engineers of the day, Thomson used the Caloric theory to show that one of the most efficient steam engines of the day was actually producing only a little more than half of its theoretical capacity.
As Thomson pondered how to resolve the conflict between the theories of Carnot and Joule, in May 1850 Rudolf Clausius (1822, d1888 ←shown at left) published a paper in Germany On the Moving Force of Heat and the Laws of Heat which may be Deduced Therefrom. Giving credit to Thomson for clarifying the ideas of both Carnot and Joule, he wrote I do not imagine that the difficulties are so great as Thomson considers them to be. Addressing the reversibility of Carnot's perfect engine, Clausius wrote It is impossible for a self-acting machine, unaided by any external agency, to convey heat from one body to another at a higher temperature. Using this Second Law of Thermodynamics, Clausius was able to prove Carnot's principle without using the Caloric theory. In the next 15 years Clausius went on to develop classical thermodynamics and publish the first book systematically presenting the whole field. Along the way he discovered a concept he later called Entropy which proved to be one of the most powerful tools of thermodynamic analysis. (Note the statistical formula Boltzmann provided for Clausius' more general concept.)
But Thomson was unable to read Clausius's paper until a year later. Meanwhile Thomson (early photo to right→) independently came to the same conclusion and published in Edinburgh in March 1851 On the Dynamical Theory of Heat, with Numerical Results Deduced from Mr. Joule's Equivalent of a Thermal Unit, and M. Regnault's Observations on Steam. In it he stated his equivalent version of what became the Second Law of Thermodynamics: It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects. He stated this was the second of two required propositions; the first, now called the First Law of Thermodynamics, is When equal quantities of mechanical effect are produced by any means whatever from purely thermal sources, or lost in purely thermal effects, equal quantities of hear are put out of existence or are generated. With the powerful theoretical support of both Thomson and Clausius built on the experimental evidence of Joule, the theory of heat based on moving molecules was established and the Caloric theory buried. And the Principle of Conservation of Energy, of which the First Law of Thermodynamics is a more limited statement, became one of the most powerful mental tools ever invented by mankind.
Einstein's paper encouraged Jean Baptiste Perrin (b1870, d1942) to pursue his experimental work to confirm the kinetic theory and show the existence of atoms. In particular Einstein predicted that the mean displacement of a grain (its random walk away from a starting position) is likely doubled over a fourfold increase in time, tenfold greater when the time is increased by a factor of 100 and so on. The mean square of the horizontal displacement increases in proportion to elapsed time. By experiment Perrin verified Einstein's prediction, virtually requiring the real existence of atoms. And so after almost two centuries, Bernoulli's kinetic theory of gas was finally accepted as reality.
Both the first and second laws of thermodynamics are observed laws: No change has ever been observed in which energy of the closed system was not conserved (the 1st law). And no spontaneous change has ever been observed which decreases net entropy of the closed system (the 2nd law). Entropy is a state function; that is, it depends only on the conditions of the system so the pathway by which it was achieved is irrelevant.
J. Willard Gibbs (b1839, d1903) developed a system which eventually led to the development of another state function known as Gibbs free energy, G, defined:ΔG = ΔHsystem – TΔSsystem
If ΔG is negative, the change will be spontaneous. If it is zero, the system is at equilibrium. If it is positive, the change will not spontaneously occur. Knowing whether a change will occur or not is very useful in many situations.
In the previous experiment you measured the Heat of Fusion, Hf, required to melt ice. In the process of melting the well organized crystal lattice in the solid ice is replaced by the more random arrangement of neighboring water molecules in the liquid. As a result the water is more disorganized as a liquid than it was as a solid. This results in a increase in entropy which can be calculated.
But the trick to obtaining enough information is to find a situation where we have a reversible situation. We know that below 0°C water freezes and is not spontaneously reversed at that temperature. Likewise at warmer than 0°C ice spontaneously melts but doesn't freeze. But if we choose to consider what happens at 0°C, we find water can either melt or freeze. So at 0°C we have equilibrium and a reversible situation. So ΔG = 0.
Note this is only a change in entropy. In one wanted to know the actual entropy at this temperature, one would have to know all processes which occur as the substance is warmed from absolute zero. (At absolute zero, there is but a single arrangement of perfect order, so W = 1.) The entropy change for each change would need to be summed. However that is rarely necessary or even useful. In practice one wants to know whether a particular change will occur, or could be forced to occur at a particular temperature. For example consider if ice could be melted 10°C colder. Knowing that temperature, the Heat of Fusion, and the entropy change, one can calculate.
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
to next experiment
to e-Physics menu
to site menu
