![]()
![]()
To understand the evolution of our ideas about heat, perhaps one should start with a brilliant, clever, daring American scoundrel prone to exaggerate.
Benjamin Thompson (b1753 in Woburn, Massachusetts, d1814) lost jobs on the dock, as a sales clerk, and as a physician's apprentice during the early revolution in Boston. He was more interested in projects such as constructing fireworks, a perpetual motion machine and a static electricity machine, and repeating Ben Franklin's kite experiment (in which Thompson was apparently struck by lightning but survived). At age 19 he married the 30 year old widow of the 60 year old richest man in Concord. Within a year he obtained a commission of major in the New Hampshire Militia from a new friend, the Governor. Accused of being unfriendly to the cause of freedom, his case was dismissed. But when faced with a mob threatening tar and feathering, he abandoned his wife and their baby forever and fled. Letters suggest he then secretly and cleverly served as a Tory spy until the British lost Boston and the 23 year old Thompson sailed for London.
 There Thompson shrewdly saved the Secretary of State for the Colonies reputation and career and in exchange was made his private secretary. Rising in power and leisure time, Thompson returned to experimentation. He used the recoil of guns and cannon hung as pendula to measure the effectiveness of different gun powder formulae. Despite criticism for claiming unwarranted originality, he did achieve election as a fellow of the Royal Society in 1781.
There Thompson shrewdly saved the Secretary of State for the Colonies reputation and career and in exchange was made his private secretary. Rising in power and leisure time, Thompson returned to experimentation. He used the recoil of guns and cannon hung as pendula to measure the effectiveness of different gun powder formulae. Despite criticism for claiming unwarranted originality, he did achieve election as a fellow of the Royal Society in 1781.
Accused that Summer of being a spy for France, Thompson abruptly departed for America with rank of Lt. Colonel to successfully raise a regiment of Americans to fight on behalf of the British. When peace was arrange two years later Thompson returned to London and seems to have used patronage to be begrudgingly promoted to full Colonel before retiring at half pay for life. After galavanting about Europe for a year as a soldier of fortune telling tales and gaining letters of recommendation, Thompson was able to return to England and persuade King George III to knight him Sir Benjamin before returning as an advisor to the ruler of Bavaria in Munich and spy for the British. In an attempt to produce better military clothing (any savings would become his profit), Thompson devised a way to measure insulators and discovered that heat can be carried away by convection currents even in clothing.
When traditional clothing suppliers were unwilling to make improvements, Thompson devised a scheme to recruit, feed, and train the local beggars to work in factories making better uniforms and to school their children. He researched meals which would be cheap but nourishing, and then utilized idle soldiers to grow the food, tend gardens and parks, and practice military training. He devised a device to measure heat from different fuels by having the exhaust smoke travel though a copper worm surrounded in a box of water of known mass and monitored for temperature changes. Thompson realized the inefficiency of cooking over an open fire so created stoves enclosing the fire. He invented the double boiler, the kitchen range, the baking oven, and advocated use of the pressure cooker. Realizing the poor illumination provided by candles, Thompson invented a device for measuring light intensity, then researched various lighting devices and fuels and devised an improved oil lamp.
At this time both heat and light were generally thought to be corpuscles similar to atoms of other elements. Antoine Lavoisier in Paris had developed a new chemistry and renamed heat as calorique and light as lumiere. It was believed that light and heat were both chemical products of combustion and were conserved just like the other chemical elements. But Thompson showed that light from candles and lamps comes from the glowing solid particles. At higher temperatures, the particles emit higher intensities of light, a clear violation of any conservation of light!
In the first 4 years in Bavaria, Thompson did little more than study the problems. But in the next 3 years he made radical changes for the army and the poor. He rapidly rose to Minister of War, Minister of Police, Major General, Chamberlain of the Court, and simultaneously State Councillor, but he created enemies during the rise. When the German emperor died in 1792, the Bavarian Elector had temporary authority and elevated Thompson to Count of the Holy Roman Empire, and Thompson chose the title of Count Rumford after the original name for Concord, Massachusetts, the town where he started by marrying the rich widow.
After 16 months of health driven travel, Count Rumford returned to do more experiments investigating heat. The calorique theory of heat successfully explained that when the element calorique flowed into a body, its volume caused the heated object to expand. And draining calorique from a cooled body resulted in the body's contraction. But Rumford had earlier been puzzled when powder fired in an empty cannon resulted in more heat than when the powder propelled a cannon shot. In his youth he had read of Boerhaave's rival theory that heat was the product of vibration in a body. Contrasting sound vibrations from a repeated rung bell with water evaporated from a wet sponge, Rumford noted the eventual exhaustion of the water but not the ability to ring because one is a substance and the other is not. He wrote further:
Being engaged, lately, in superintending the boring of cannon, in the workshops of the military arsenal at Munich, I was struck with the very considerable degree of Heat which a brass gun acquires in a short time, in being bored; and with the still more intense Heat (much greater than that of boiling water, as I found by experiment) of the metallic chips separated from it by the borer. (Early on he found the chips removed by drilling still had precisely the same heat capacity as the original metal!)Being responsible for supervising the drilling of cannon in Munich, Rumford arranged to have cannon bored in a tank of water, measuring the time to heat the water from room temperature to boiling. Repeated many times, Rumford found no signs of calorique being exhausted or even diminished as that theory required from the process draining heat embedded in the metal. He wrote:
The more I mediated on these phenomena, the more they appeared to me to bid fair to give a farther insight into the hidden nature of Heat; and to enable us to form some reasonable conjectures respecting the existence, or non-existence, of an igneous fluid; a subject on which the opinions of philosophers have, in all ages, been much divided.
It is hardly necessary to add that anything which any insulated body, or system of bodies, can continue to furnish without limitation, cannot possibly be a material substance; and it appears to me to be extremely difficult, if not quite impossible, to form any distinct idea of anything capable of being excited and communicated in these Experiments, except it be Motion.
So Count Rumford effectively removed both lumiere and calorique from Lavoisier's new list of chemical elements. Neither light nor heat are substances.
 Returning to England to popularize his ideas of reform to improve efficiency of society, Rumford rode a wave of popularity. (←caricature by James Gillray at left) While in London he noted the dark smoke which hung over the city was wasted, unburned coal dust, so he modified fireplace chimneys by narrowing the throat, adding a shelf to block smoky downdrafts, and adding a damper to close when there were no fires. Realizing that a fireplace heats by little understood radiation, Rumford did a series of investigations where he found that polished bodies do not radiate well, but that rough, sooty bodies radiate much better.
Returning to England to popularize his ideas of reform to improve efficiency of society, Rumford rode a wave of popularity. (←caricature by James Gillray at left) While in London he noted the dark smoke which hung over the city was wasted, unburned coal dust, so he modified fireplace chimneys by narrowing the throat, adding a shelf to block smoky downdrafts, and adding a damper to close when there were no fires. Realizing that a fireplace heats by little understood radiation, Rumford did a series of investigations where he found that polished bodies do not radiate well, but that rough, sooty bodies radiate much better.
When the French and Austrians went to war, Rumford was summoned back to defend Munich as the entire royal court and heads of state fled presuming imminent conquest of the city. Rumford negotiated with both armies to camp outside the city, and when after weeks of Rumford's daily shuttle diplomacy the French lost elsewhere, both armies withdrew leaving Rumford a hero without a shot being fired. During the siege for the city, food and fuel were in short supply, so Rumford developed an efficient portable stove and managed to feed both his garrisoned army and the city population. But his Bavarian political enemies eventually forced his departure, and a Bavarian appointment to England managed to offend King George III as well.
After working to establish two prizes to promote creative scientific efforts, Rumford offered to establish a military academy for the United States. They arranged for him to tactfully decline their acceptance of his offer! He then established the first science museum devoted to educating the public, charted as the Royal Institution of Great Britain. The second director appointed by Rumford, Humphry Davy developed it into a great institution. Noteworthy among opposition to the public presentation of scientific discoveries was James Watt, who was trying to protect his expiring patent on an efficient steam engine.
On a quick trip back to Munich, Rumford returned by way of Paris where he met Marie Lavoisier, the rich and fashionable widow to the guillotined chemist. At age 25, Antoine Lavoisier had married 13 year old Marie. Her skills and those she learned complimented those of Antoine so they became very compatible, productive partners. Leaving England for the last time, Rumford conducted a 4 year courtship of Marie. But both Rumford and Marie had formed hardened opinions with age. Despite the long courtship, they soon found marriage difficult and separated within 2 years. Rumford continued to do scientific experiments and contributed to the French Academy of Sciences. Thinking that there might be a better beverage than alcohol which sometimes creates discord, Rumford invented the drip coffee pot to consistently brew coffee without destroying by boiling or otherwise losing the essential flavor oils. Count Rumford died suddenly in 1814, leaving his estate to endow a professorship at Harvard University back in America.
Heron of Alexandria about 100 A.D. first demonstrated steam power with a lawn sprinkler type device which rotated when steam exited nozzles attached on opposite sides of a revolving boiler. But steam power remained a novelty until the British made it practical and commercially successful. Thomas Savery (b1650, d1715) patented a fire engine in 1698 using high pressure steam to pump water from English mines. Savery's engine used a two step process where the steam pressure forced water from a collection chamber up a pipe to where it could be drained away at ground level. That completed, the steam was blocked and cold water cooled and condensed the steam in collection chamber drawing more mine water into the chamber (pushed by atmospheric pressure). Then the steps were repeated. He set us a factory and promoted the sales of such engines in 1702. But Savery's engine carried risk of steam pressure getting too great and exploding the collecting chamber or the boiler. It was very inefficient, but fuel was abundant and there were no alternatives other than work animals.

Ten years later the safety issue was remedied by another Englishman, Thomas Newcomen (b1663, d1729) who with his manufacturing partner, John Calley, introduced a close fitting piston in a uniform cylinder, coupled to a rocking beam to lift either water or other loads. Its use of much lower pressure steam reduced the risks of explosion. Early models required a person to monitor progress and open and close valves to alternate from compression to cooling and condensation. Later feedback devices were designed so that the motion of the engine actually opened and closed the valves at key times in the cycle. Still the cycle of heating and cooling the cylinder was slow and rather inefficient. When the primary patents expired in 1733 other companies also produced similar steam engines and refined the design. As a result the Newcomen engine was widely used in Britain and on the European continent during the 18th Century.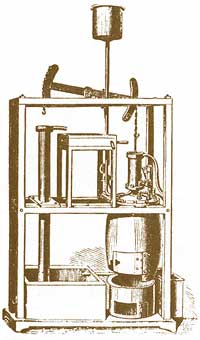
James Watt (b1736, d1819), son of a Scottish carpenter, studied to become an instrument maker in London then returned to such a job at the University of Glasgow. Over the winter 1763-64 Watt was asked to repair the University's demonstration Newcomen engine (diagram of that engine at right→) which had never worked properly. Acquainting himself with how the model functioned, he undertook a series of experiments and discovered that much heat was required, most of which went to warming the cylinder walls, only to have them cooled with water each cycle. Early in 1765 Watt devised an improved steam engine which moved the cooling and condensing function to a separate chamber. This allowed the cylinder to remain hot and the condenser to remain cold, allowing for much more efficient and speedy operation. Watt teamed up with engine manufacturer Matthew Boulton to produce and sell such engines. In order to compare their improved engines with those of the predecessors, they defined, measured and advertised the horsepower of their Watt steam engines. Power is the rate of doing work; that is, the amount of energy transformed to useful service divided by the elapsed time.
With the calorique theory of heat in doubt, considerations of such engines as that designed by Watt suggested to a few scientists that heat should be considered a form of energy. Chemical energy contained in the fuel would be passed as heat to the steam, and then via the moving piston into mechanical energy which was a combination of kinetic and potential energy. The efficient Watt engine could be used in traditional stationary situations to lift materials loads, or in mobile situations to drive steam powered boats or for land transportation. Because the steam engine with its supply of fuel, water, boiler, piston, and condenser were heavy, such engines often required the support of rails to prevent the vehicle from sinking in muddy or sandy land. But the design of the steam engine remained largely a matter of trial and error rather than an understanding of the underlying science.
Not until 1842 did J.R. Mayer published in Germany a paper postulating the general equivalence and conservation of all forms of energy. But his paper received little attention at the time. The English physicist James Prescott Joule (b1818, d1889) published in 1829 the results of experiments he conducted in the 1840s gathering a large body of convincing evidence that heat is a form of energy. He concluded:1st. That the quantity of heat produced by the friction of bodies, whether solid or liquid, is always proportional to the quantity of energy expended.
And 2nd. That quantity of heat capable of increasing the temperature of a pound of water ...by 1°Fahr. requires for its evolution the expenditure of a mechanical energy represented by the fall of 772 lb through the distance of one foot.
In 1847 William Thomson (b1824, d1907) crossed paths with James Joule at a meeting of the British Association in Oxford. Joule argued that heat was due to the vibration of a material's atomic constituents. By studying the decrease in volume of a gas as it was cooled, Joule suggested that no substance could be colder than a temperature of -284°C. Thomson became fascinated by Joule's claims. Asking questions from the floor, he provoked a lively debate, but assumed that Joule's claims likely were flawed. But after careful consideration, Thomson came to agree with Joule. Thomson connected Joule's work with that of Sadi Carnot on heat engines, and devised a more fundamental way of defining absolute zero temperature independent of any particular material substance and in 1848 proposed a thermodynamic (absolute) temperature scale. As a result the fundamental unit of temperature was later called the Kelvin, after the name Baron Kelvin of Largs which Thomson adopted when he was made a Lord in 1892. Thomson also saw the idea of conservation of energy as a great unifying principle in science, and introduced the ideas of statical and dynamical energy, what are now call potential and kinetic energy. Thomson, Clausius, Helmholtz, Joule, Liebig, Carnot and Rankine all contributed to our understanding of heat and the first and second laws of thermodynamics.
The first law of thermodynamics is an expression of the universal law of conservation of energy, and identifies heat transfer as a form of energy transfer. The increase in the internal energy of a thermodynamic system, ΔU, is equal to the amount of heat energy added to the system, Q, minus the work done by the system on the surroundings, W:HEAT EXCHANGE = SHARING the ENERGY: When two or more objects at different temperatures are brought in situation with no outside influence, they eventually reach the same temperature. The warmer body transfers heat to the colder body. The energy which is being transferred is called the internal energy, energy associated on the microscopic scale with the random motion of the molecules. This energy includes both kinetic energy and the potential energy due to chemical bonding in the material. If we have two isolated bodies and no loss or gain to the environment, then conservation of energy principle requires that the heat lost by one substance, Q, must be gained by the other:
Qlost = Qgained
Since temperature is a measure of the average kinetic energy of the random molecular motions, as a body gains or loses kinetic energy its temperature will increase or decrease. The temperature change, (Δ is the 4th capital letter in the Greek alphabet, pronounced delta, perhaps chosen because it resembles the shape of rather frequently changing river deltas.)Although the internal energy in an object is directly proportional to its mass, two objects of different composition may have different internal energies even if they have the same mass and temperature. Temperature reflects only the kinetic energy portion of the internal energy, so different substances may have differing amounts of potential energy and therefor different total internal energies at the same temperature. For example, a gram of water at 50°C has a much larger internal energy than a gram of Copper at 50°C. As a result it requires a larger amount of energy to heat water to 60°C than to produce the same temperature change in an equal mass of Copper. This is measured in a property called the specific heat, Cp (heat Capacity at constant pressure), defined as the quantity of heat required to raise the temperature of 1 gram of a substance 1°C.
The quantity of heat lost or gained by a body can be calculated byIn the past energy was typically measured in calories defined by the amount of heat needed to raise the temperature of 1 gram of liquid water 1°C. The food industry still uses a dietary Calorie which is actually a kilocalorie or 1000 calories. (note the CAPITAL C, although not always used on food labels, perhaps due lack of technical training in the advertising industry of the difference between cal and Cal.) But most of the rest of the world changed to the System International units in the mid-20th Century where energy is measured consistently in units of Joules. While the Joule is defined from more fundamental units ( Joule = Newton • meter ), 4.184 J of heat will warm 1 gram of liquid water 1°C.
The first investigation determines the specific heat of a sample (perhaps of metal). A heated sample is immersed into cool water in an insulated container. With care taken to prevent heat from entering or escaping this insulated container, it is assumed that the amount of energy lost by the hot sample is gained by the water. From the equations above the amount of heat gained by the water can be computed. Since this must be the amount of heat lost by the sample, the specific heat of the sample, can be calculated. You will need a way to measure water temperature and volume, and a way to determine the sample's mass.
CHANGE OF PHASE: Originally the Greeks thought that solids, liquids, and gases represented elementary differences. But Antoine Lavoisier (b1743, d1794, Marie's 1st husband) proposed that a single material can exhibit these different phases by merely a change in temperature. We now consider these to be different states of existence. Beyond these common phases, many substances have several different solid phases which occur at different temperature and pressure ranges. Generally they are related on the microscopic scale to different crystal packing arrangements of their atoms or molecules. But here we are interesting in the energy difference between one phase and another. In the next investigation we will try to relate this energy difference to otherwise hidden differences in entropy, or conversely, the packing organization in the material. Generally an increase in internal energy is required to convert a solid to a liquid. Conversely, a reduction in internal energy can cause liquids to freeze (solidify). These solid-liquid phase changes occur without a change in temperature, that is, with no change in average kinetic energy occurs. For example, the molecules in ice at 0°C are moving just as fast on average, with the same kinetic energy, as liquid water at 0°C! Their average speeds only change if they are at higher or lower temperature. The heat of fusion of a substance is the heat exchange required to melt one gram of the substance (Joules/gm).
In this part of the experiment, the heat of fusion of water will be determined. Warm water will be used to melt ice, and the change in temperature of the water in an insulated container. Such a device is commonly called a calorimeter. Very expensive calorimeters can be purchased, but results nearly as good can often be obtained in a colorimeter as simple as an inexpensive styrofoam cup! A paper container nested inside a second container is not likely as well insulated, but can also provide reasonable results, and considerable insight into the science of calorimetry. The ice must absorb heat in order to melt. The heat absorbed can be expressed as
Heat gained by ice = Heat lost by original liquid water
mice Hfusion + mice ΔTice water = Cp mwater ΔToriginal liquid
where Hfusion is the heat of fusion in Joules/gram. The necessary heat will be transferred from the warm water to the ice. If any ice remains unmelted and is removed, the light gray term vanishes. In either case we need to calculate the amount of ice which actually melted, mice. But if we use more liquid water, the ice will all melt and the THAT ice water will warm a bit requiring we subtract the gray term from both sides of the equation.
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
![]()
to next experiment
to e-Physics menu
to site menu