It's love that makes the world go round. ancient ditty
Energy makes the World go round. ENERGY explains EVERYTHING. modern ditty
It is an easy claim that Energy is so important, but such a claim can be practically meaningless. For energy to have meaning and value, one needs to understand how that concept was developed. The value of energy grows as you gain understanding of the various forms of energy, how it is calculated, and how such measurements are useful. With energy a term in wide popular use, this and many of the following experiments will describe how aspects of energy were proposed to increase our understanding. With modern society depending on energy containing fuels and survival of all life requiring energy, often in the form of food, the importance of energy may seem obvious. But little of that importance was apparent when scientists first suggested a need for such a concept.
While observations suggest that conservation of momentum, mv, is always true in every closed system (where no momentum is robbed away or introduced from outside forces) there are more possibilities than nature seems to permit. For example Experiment III-2's procedure B gave evidence that the number of balls moving after a collision was the same as the number moving before (as in diagram below). This conserves momentum, but one could envision additional situations which also conserve momentum. For example (1) after the collision twice as many balls might move with half the speed, or (2) half as many balls might move with twice the speed. But those situations are NEVER observed. Perhaps there is some additional property which, by also being conserved, precludes those other envisioned collision outcomes?
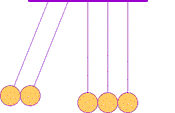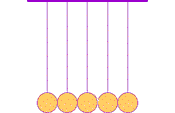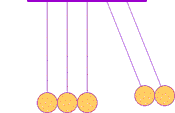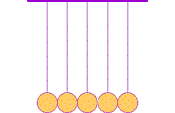In 1666, two decades before publication of Isaac Newton's Principia, the phenomena was demonstrated to the Royal Society using a series of hard balls hung next to each other from strings as pendulums. In Holland Christian Huygens (b1629, d1695 portrait at right→) proposed the conservation of both momentum and another property, which he termed vis viva, calculated as mv2. If both properties are conserved, only a single, unique set of motions will be allowed as a consequence of any collision. For the first time, the world had an understanding of such collisions that matched what was observed. And more importantly, conservation of both vis viva and momentum preclude what NEVER happens.
But much remained to be explained. Situations with less than fully elastic collisions did not perfectly match the theory. Not until the mid-19th Century did a group of European physicists developed a consistent set of energy definitions which established the Conservation of Energy which holds in every closed system. For logical consistency, they defined kinetic energy as ½mv2, supplanting the experimental property of vis viva.
Inertia means that a rolling ball on a smooth, level surface will roll forever if nothing stops it. In fact, friction and air pushing against the moving ball will eventually bring it to a stop. But interesting things happen when a motionless object gets in the way of a moving one. If you have data from Experiment III-2's procedure B, you may wish to use that rather than obtaining measurements as follows:
1 marbleand speed,
1 arbitrary speed unit.)
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
Several experiments ago it appeared that mass is conserved. But while Albert Einstein pondered some of the apparent paradoxes of our universe, he discovered that mass is apparently a form of energy. In an exothermic reaction where heat is released, a tiny amount of mass should be the source of energy in the proportion E = mc2. So we've modified our ideas about both mass and energy.
Now that we have added kinetic energy to help explain our observations, we might wonder if there are more forms of energy? Following investigations will add forms of energy associated with a variety of forces. In recent years scientists have hypothesized both dark matter and dark energy! The scheme of science has been to imagine a new brand of energy whenever we find energy either vanishing or appearing from nowhere. This may look dishonest: sort of like a banker inventing fictitious customers to cover discrepant bank records! But it is not wicked, since we publish our assumptions honestly and, knowing our procedure is risky, set out to find verifying evidence. Looking back in the history of science, such risks have been taken before and have turned out to be magnificently justified. In the early 1800s a proposal that heat is a form of energy seemed strange. But as we shall see, experiments eventually found it the better explanation. The neutron, now an essential ingredient in nuclear reactors, was discovered through a misfit in measured energies. An energy-accounting problem appeared in radioactive beta decay where ejected electrons do not emerge with identical kinetic energies but ranging from zero to a apparent maximum, leaving a large, variable, chunk of energy missing. So physicists invented another tiny particle, the neutrino, with no charge and almost no rest-mass so it leaves many nuclear reactions without detection, carrying amounts of kinetic energy, momentum, and spin to conserve all those endangered concepts. A wicked invention? What might lead to great experiments and growth of knowledge might also seem to be a bogus way to deal with observations and measurements that existing theory can't explain. In fact, experimental evidence now suggests that three forms of neutrinos are genuine.
We return to the key question: Is energy purely an experimental thing with its universal conservation experiment based? Or is it a hypothesis that we have dreamed up and agreed on, and will try to maintain? In a great many situations, conservation of energy has been supported by a large number of experiments. If energy was just wild speculation and day dreaming by scientists, inconsistencies and contradictions would have been found long ago. But in its present fullest form you may consider it more than a generalization from experiment; it has expanded into a convention, an agreed scheme of viewing the world. If you feel disillusioned, read the following remark by Jules Henri Poincaré (b1854, d1912), one of the greatest mathematical physicists: As we cannot give a general definition of energy, the principle of the conservation of energy simply signifies that there is something which remains constant. Well, whatever new notions of the world future experiments may give us, we know beforehand that there will be something which remains constant and which we shall be able to call energy. (La Science et I′Hypothèse, 1902)
While the debate whether energy is real shall continue, it might be worth remembering its origins in the proposals and formulas of human minds. Regardless of the debate outcome, beyond dispute is the immense value of the logically consistent concepts of energy.
to next experiment
to e-Physics menu
to site menu
