ie-Physics

summary and practice

© by William Dietsch 2005

The Nature of Light

Visible light is the range of electromagnetic waves which can be seen by human beings.   Those wavelengths range from 3.8 x 10^-7 to 7.5 x 10^-7 meters.   The shortest visible wavelength is the color violet.  The spectrum of colors range continuously through what we call indigo, blue, green, yellow, orange, and red.   Ranges of electromagnetic radiation with wavelength longer than red are known as infrared and shorter than violet are known as ultraviolet.   These wavelengths are just a small segment of the entire electromagnetic spectrum.

The behavior of light sometimes suggests that it is composed of particles and sometimes it is considered to be carried as waves.   The modern electromagnetic theory of light considers light as particles called photons, which display all of the attributes and characteristics of waves.

The speed of light (c) in a vacuum is the absolute maximum speed of anything in the universe.   The maximum speed of light, that through a vacuum, is 3 x 10⁸ m/s.   The speed of light was first determined by the astronomical observations of Ole Roemer in 1674.   The modern and accepted accurate value was determined by an experiment performed by Albert Michelson in 1926 using a rotating mirror and a beam splitter.   The speed of light is one of the most important constants in modern physics.   

Production and Transmission of Light

Objects can be visually perceived when light from them reaches a human eye.   Luminous objects produce light and as a result can be seen.   stars and light bulbs are examples of luminous objects.   Illuminated objects reflect light and are seen by the light, which comes from their surfaces, by reflection.   Surfaces, which scatter the light, are producing diffuse reflection.   Surfaces (such as mirrors) which reflect light in an organized way display specular reflection.

The intensity, I, of a light source is measured in units called candela (cd)

The rate at which light energy is produced by a luminous source is the luminous flux, Φ.   Luminous flux is measured in a unit called the lumen.   Φ = 4 π I

The density of light falling on a surface is called illuminance, E.   This is a more useful measure of the amount of light.   Illuminance is measured in lumens/m², more often called lux.   The formula for determining illuminance (or illumination of a surface) is: E = Φ / 4 π d², or E = I / d² where Φ is the luminous flux measured in lumens, I is the intensity in cd, and d is the distance from the surface to the source measured in meters.

Optical Reflection

The regular (specular) reflection of light rays from surfaces (usually mirrors) is a useful tool in the production of optical devices.

The law of reflection governs the behavior of reflected rays from regular (smooth) surfaces.   The law of reflection states that the angle of incidence (incoming light ray) is equal to the angle of reflection (reflected light ray).  The angles are measured from a normal line (perpendicular) drawn to the surface at the point of reflection.

Mirrors are optical devices, which use reflection to manipulate light.   Plane mirrors have flat surfaces. Curved mirrors have surfaces, which are curved, for the purpose of reflecting light for some advantage.   Curved mirrors are most often spherical or parabolic.   Concave curved mirrors reflect light from the inside of the curved surface and convex mirrors reflect light from the outside of the curved surface.

Images are produced by the intersection of reflected light rays which originating from an object.   Light rays which converge from a concaved mirror intersect in front of the mirror and form a real image.   If the reflected rays diverge in front of a convex, flat, or sometimes a concaved mirror, the mind imagines where it appears they came from, a virtual source.   The intersection of these extended rays produce an image, constructed by the mind, which appears behind the mirror, a physical impossibility, is called a virtual image.  Real or virtual are terms used to describe the character of the image.   If the image is in the same orientation as the object (right side up) it is called an erect image.   If the image is upside down it is called an inverted image.   Erect and inverted are terms, which describe the attitude of the image.   If the image appears smaller than the original object it is reduced and if it appears bigger than the original object it is enlarged.

Optical Refraction:

Refraction is the bending of light rays as they pass from one medium to another at an oblique angle.   The two media must have different optical density (i.e., the speed of light is different in each medium).

Light rays bend toward the normal when passing from less dense materials (having the faster light speed) to more dense materials (where light travels slower).   The opposite occurs when the light moves from more optically dense to less optically dense media.

The ratio of the speed of light in a vacuum to the speed of light in a substance is called the absolute index of refraction, n, for that substance.  n = 3.00 x 10⁸m/s / speed in the substance).  (n for every real substance is greater than 1.)

Snell's Law of Refraction states that a ray of light bends in such a way that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant.   Snell's law gives another definition of the index of refraction: n = (sin θ_i) / (sin θ_r).   This gives the relative index of refraction.   If the incident medium is a vacuum (air is close), the relative index is equal to the absolute index.   Another form of Snell’s law: n₁ sin θ₁ = n₂ sin θ₂.

When light passes from a material, which has an absolute index of refraction higher than the material into which it is passing, the angle of refraction is greater than the angle of incidence.   When the angle of refraction equals 90°, the incidence critical angle is reached.   The critical angle does not allow any light to pass through the interface between the media because the refracted ray is parallel to the boundary.   Exceeding the critical angle causes the light to undergo total internal reflection.  This property of total internal reflection is used in light pipes and fiber communication bundles to keep all light inside (except at the ends) despite the material having gradual bends.

Lenses are curved objects made of a transparent material, which are cleverly designed to take advantage of refraction to bend the path of light in a controlled manner.   Lenses, which are thicker in the middle than at the edge, are called convex or converging lenses.   Lenses, which are thinner in the middle than at the edge, are called concave or diverging lenses.   Images formed by convex lenses are similar to images formed by concave mirrors.   Multiple lenses are assembled in appropriate combinations by clever engineers to produce optical devices such as microscopes, telescopes, binoculars and other devices to aid our sight.

Diffraction And Interference Of Light

When light passes through slits, which are very narrow, or through two or more slits, which are close to each other, they display diffraction.   Diffraction is the spreading out of the light waves after passing through a narrow opening in a barrier or the edge of a barrier.   When light passes through narrow slits, a pattern of light and dark lines appears due to interference between the diffracted waves.   The dark lines are due to complete destructive interference of the light waves and are called nodes.   The illuminated parts of the diffraction pattern are due to constructive interference and are called antinodes.

Single slit diffraction: When light passes through a single slit, bands of light and dark appear.   In the following equation, x is the distance between the center of the first illuminated band and the adjacent dark band, λ is the wavelength of the light, w is the slit width and l is the distance from the slit to the screen (all measure in m or any uniform length unit):

x = l  λ / w

Double slit diffraction: When light passes through a pair of small slits close together, a series of light bands flank the sides of the center illuminated band.   In the following equation, x is the distance between the central band and the adjacent first order band, d is the separation between the slits, λ is the wavelength of the light, and l is the distance from the slit to the screen (all measure in m or any uniform length unit):

x = l  λ / d

When white light passes through a diffraction array, each color is deflected a different amount producing a continuous spectrum of color.   When monochromatic (only one color) light passes through a diffraction array, a pattern of nodes and antinodes will appear in this single color. The equation above for double slits is also valid for diffraction gratings, except that d represents the slit spacing (m).

Practice Problems On Light

1. What is the frequency of light with a wavelength of 641 nm?   (n = nano is the prefix equivalent to 10^-9.)
   
   
2. How long will it take light to move from one end of a football field to the other?  (d = 100 m)
   
   
3. A light pulse is bounced off the moon.   The time that it takes for the light to make the round trip is 2.562 s.   Compute the distance from earth to the moon in meters.  (The moon has an orbit eccentric of 0.0549 so this time varies.)
   
   
4. The distance from the earth to the sun is 1.5 x 10⁸ km.   Compute the time that it takes for light from the sun to reach earth.  (The earth has an orbit eccentric of 0.0167 so this distance varies.)
   
   
5. How long would a radio signal traveling at the speed of light take to reach Pluto from the earth if the distance between them is 5.75 x 10⁹ km?  (How much would this vary in a year?)
   
   
6. What is the illumination on a surface 3.2 m from a lamp, which has a luminous flux of 3125 lm?
   
   
7. The illumination falling on a surface is 20.0 lx.   The light source is located 3.5 m from the surface.   Compute the luminous intensity of the source.
   
   
8. Local law requires the illumination on a school desk to be at least 160 lx.   If the lights are located 2.00 m above the desk, compute the luminous flux required of the light fixtures.
   
   
9. Compute the illumination 4.00 m below a 405 lm lamp.
   
   
10. Two lamps illuminate a screen equally.   The first lamp has an intensity of 105 cd and is located 5.4 m from the screen.   The other lamp is located 3.1 m from the screen.   Compute the intensity of the second lamp.
    
    
11. A 12 cd lamp and a 65 cd lamp cast equal intensities on a screen.   If the 12 cd lamp is 6.2 m from the screen, how far is the 65 cd lamp?
    
    
12. A ray of light has an angle of incidence of 30.0° on a block of transparent material.   If the angle of refraction is 21.0°, compute the index of refraction of the material.
    
    
13. A ray of light has an angle of incidence of 30.0° when passing from air into a liquid.   Compute the index of refraction of the liquid if the angle of refraction is 24°.
    
    
14. A ray of light has an angle of incidence of 60.0° when passing from air into flint glass.   Compute the angle of refraction.
    
    
15. Look up the index of refraction of water.   Compute the speed of light in water.
    
    
16. The speed of light is 2.66 x 10⁸ m/s in a material.   Compute the index of refraction of the material.
    
    
17. Compute the critical angle when light passes from crown glass into air.
    
    
18. Compute the critical angle when light passes from flint glass into water.
    
    
19. How many minutes longer would it take light from the sun to reach earth if the solar system were in a huge flint glass paperweight?   Hint: the distance from the sun to the earth is 1.496 x 10¹¹ m.
    
    
20. Light falls on a pair of slits 1.90 x 10^-5 m apart.   The slits are .800 m from the screen.   If the first order bright line is .0190 m from the central bright line, compute the wavelength of the light.
    
    
21. Light of a wavelength of 548 nm falls on a double slit.   The first order line is 4.00 cm from the central bright line and the screen is 1.20 m from the slits.   Compute the distance between the slits.
    
    
22. Light falls on a single slit with a width of .010 cm and falls on a screen 1.00 m away.   If the distance from the center of the pattern and the first bright band is .600 cm, compute the wavelength of the light.

Optical Reflection

Concave Mirrors:

23. Complete the ray diagrams below to determine the images of the object arrows as viewing in concaved mirrors.

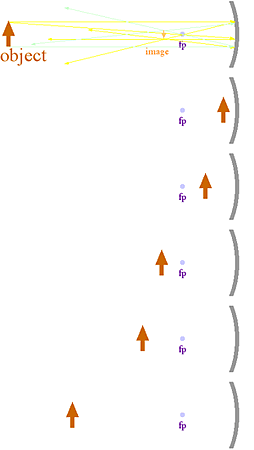Ray optics is an exercise in Euclidian geometry (Euclid of Alexandria, Egypt,  f300BC), adopted for understanding the paths of light rays.  It assumes that light travels in straight lines unless its path is changed by reflection or refraction.  Light rays approaching from different directions reflect of a curved mirror in a wide range of directions.  However by selectively choosing several well located light rays, the behavior of the mirror can be understood and the paths of a large number of other light rays determined. Using a distant light source (e.g., the Sun) and a small screen, determine the focal point of the concaved mirror.  Ideally such a mirror should have a parabolic shape however a small section of spherical shape is often used as a less expensive compromise.  The focal point can be approximated by a point half way from the mirror's surface to the center of curvature. To construct a diagram for an object located in front of a concaved mirror, consider a light ray originating say at the top of the object directed parallel to the central axis of the mirror.  According to the law of reflection, this will reflect off the mirror in the direction passing through the focal point.  Conversely, a ray with the same origin directed through the focal point will reflect off the mirror parallel to the central axis. Another ray with the same origin passing through the center of curvature will strike the mirror perpendicular and be directed back along the same path through the center of curvature. These outward reflected light rays may focus where the rays cross, producing there a real image of that part of the object.  If however the outward rays diverge after reflection, they can be imagined to extend backwards to where a virtual image of that part of the object would seem to be located. This process can be repeated for light rays originating at other parts of the object, say its foot, to find the location of the images of those parts of the object.

Convex Mirror:

24. Draw a ray diagram illustrating the formation of an image from an object shaped like an upward pointing arrow as viewed in a convex mirror.  (Hint: use the same focal point and rules as if light could approach the reflecting surface from the back, concaved side.)
    
    
25. Complete the chart below.
    
    

selection of descriptions for image

real – formed by light rays which intersect in space in front of the mirror.
virtual – formed by light rays which intersect when traced back behind the mirror.

the actual location of the image

inverted – upside down
erect – right side up

enlarged – larger than the object
reduced – smaller than the object
same size

Lens Optics

Convex Lenses:

26. Complete the ray diagrams below to determine the images viewed of the object arrows.

Ray optics can be used to approximated the paths of light passing through thin lenses using rules similar to those used to understand curved mirrors.  Generally light rays refract passing through both surfaces of a curved lens.  By selectively choosing several well located light rays, the effect of the lens on the path of light can be understood. Using a distant light source (e.g., the Sun) and a screen, determine the focal point of the convex lens.  For thin lenses there are two focal points located equal distance from the lens along the axis of the lens but on opposite sides. To construct a diagram for an object as seen through a convex lens, consider a light ray originating say at the top of the object directed parallel to the central axis of the lens.  This light ray will travel more slowly in the lens resulting in the path refracting in a direction passing through the focal point.  A ray with the same origin directed through the near focal point will refract passing through the less, exiting parallel to the central axis. Another ray with the same origin passing through the center of a thin lens will approximately pass straight through. These outward refracted light rays should focus where the rays cross, producing there a real image of that part of the object.  If however the outward rays diverge after refraction, they can be imagined to extend backwards to where a virtual image of that part of the object would seem to be located. This process can be repeated for light rays originating at other parts of the object, say its foot, to find the location of the images of those parts of the object.

Concave Lens:

27. Draw a ray diagram illustrating the formation of an image from an object shaped like an arrow.
    
    
28. Complete the chart below.

selection of descriptions for image

real – formed by light rays which intersect in space opposite lens from object.
virtual – formed by light rays which intersect when traced back to object's side of lens.

the actual location of the image

inverted – upside down
erect – right side up

enlarged – larger than the object
reduced – smaller than the object
same size