![]()
The energy, which flows, from one body to another because of their temperature difference. If two bodies have the same temperature as a third, they will be in thermal equilibrium with each other and no heat will flow. This fact is often refereed to as the zeroth law of thermodynamics. +ΔQ refers to heat which flows from a system and -ΔQ indicates heat flow into a system.
Refers to the total energy content of a system. It is the sum of all the kinetic, potential, electrical, nuclear and all other forms of energy possessed by the molecules of a system. The internal energy of an ideal gas is purely kinetic and depends only on the temperature of the gas.
When a system does work to its surroundings, ΔW has a positive sign. If the surroundings do work on a system, ΔW has a negative sign.
The first law is a statement of the principle of conservation of energy. It states that if an amount of heat energy (ΔQ) flows into system, then this energy must appear as an increase in the internal energy (ΔU) and or work (ΔW) done by the system on its surroundings. (preferable units are Joules)
ΔQ = ΔU + ΔW
A process carried out at a constant pressure. See below.
A process carried out at a constant volume. When a gas undergoes such a process, any heat, which flows into the system, appears as an increase in the internal energy of the system, i.e., ΔQ = ΔU. See below.
A constant temperature process. In the case of an ideal gas, ΔU = 0. This in not true for all systems. For example, when ice melts the change in internal energy is not equal to zero because the change of state requires energy input to the ice to change its state (latent heat of fusion). For an ideal gas under isothermal conditions, (i.e., ΔU = 0) all work input is equal to an increase in the thermal energy. (ΔQ = ΔW). See below.
One in which no heat energy is transferred to or from a system. ΔQ = 0). Any work done by the system is done at the expense of the internal energy (0 = ΔQ = ΔU + ΔW).
The ideal efficiency of a heat engine is defined as: ε = work output/work input.
The Carnot cycle by Nicolas Léonard Sadi Carnot (b1796 in Paris, d1832) is the most efficient cycle possible for a heat engine. An engine in accordance to this cycle operates between a hot reservoir (at temperature Th) and a cold reservoir (at temperature Tc). (The temperatures are absolute, preferably expressed in Kelvin.) The efficiency, ε = 1 - Tc / Th.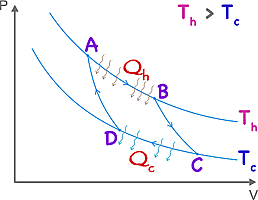
A → B The gas is first (this is a cycle, so our start is arbitrary) expanded isothermally by the addition of heat Qh.
B → C The gas then expands adiabatically. No heat enters or leaves the system but the temperature drops from Th to Tc.
C → D The gas is compressed isothermally (constant temperature Tc) and heat flows out Qc.
D → A The gas is compressed adiabatically. No heat enters or leaves the system, but the temperature increases to the original measure.
The area encompassed by the enclosed curves on the graph represents the work done by the engine.
If the first and third steps are done infinitely slowly the process is theoretically reversible.
A real process on the other hand is not completed slowly and therefore results in an irreversible process. In practical applications, heat can be supplied by a fuel and external work performed. Or the cycle can be reversed using an external source of work, pumping heat out into the warmer environment as in a refrigerator.
Heat flows spontaneously from a hotter to a colder object, but not vice versa. This is the Clausius statement of the second law.
No device is possible whose sole effect is to transform a given amount of heat completely into work. This is the Kelvin-Planck statement of the second law.
If a system undergoes spontaneous change, it will change in such a way that its disorder will increase, or at best remain the same.
If a system undergoes spontaneous change, it will change in such a way that its entropy will increase, or at best remain the same.
The second law tells us the direction a spontaneous change will follow, while the first law tells whether or not the change is possible according to energy conservation. Sometimes the second law is used to determine time’s arrow. That is, the increase of entropy and decrease of available energy in a system is an indicator of the spontaneous processes that we use to measure the passage of time.
Entropy is a state variable for a system at equilibrium. This means that the entropy (S) is always the same for a system at equilibrium. When heat (ΔQ) enters a system at absolute temperature T, then the change in entropy is: ΔS = ΔQ/T. A reversible change is one in which the values of p, V, T, and U are well defined during the change. If the process is reversed then the values of p, V, T, and U will follow the same values but in reverse order thorough the change.
Another fully equivalent definition of entropy can be given from a detailed molecular analysis of the system. If a system can achieve the same state in Ω different ways (different arrangement of the molecules etc.) then the entropy of the system can be expressed: S = k ln Ω. Where k is Boltzmann’s constant (1.38 X 10-23 J/K) and ln is logarithm to the base e.
A system that can occur in only one state (only one arrangement of the molecules for example) has a high state of order and a low state of entropy. To associate a number with disorder, the disorder of the system is proportional to Ω (the number of possible ways that state can occur). Spontaneous processes in systems containing many molecules always proceed from a state of order to a state of disorder. Entropy never decreases in a spontaneous process; it always increases or stays the same.
Is that state of a system, in which the entropy has a maximum value. It is the state with the maximum disorder and the state that can occur in the largest number of ways.
Ludwig Boltzmann (b1844, d1906) made a clear distinction between the gross properties of a system such as pressure, temperature, and volume (macrostate), and the microstate of the substance. The microstate of the substance would be ascertained by determining the position and velocity of all of the molecules making up that system. There are lots of microstates, which can yield the same macrostate. Consider the possible microstates in which only four coins are tossed as shown in the following table.
|
Macrostate |
Possible Microstates |
Number of microstates, Ω |
|
4 heads |
HHHH |
1 |
|
3 heads, 1 tail |
HHHT, HHTH, HTHH, THHH |
4 |
|
2 heads, 2 tails |
HHTT, HTHT, THHT, HTTH, THTH, TTHH |
6 |
|
1 head, 3 tails |
TTTH, TTHT, THTT, HTTT |
4 |
|
4 tails |
TTTT |
1 |
Below is a table for 102 tossed coins. After noting the number of microstates for a hundred coins, consider the vast numbers of microstates to the locations of molecules in a balloon of gas (recall a mole of gas contains 6 x 1023 molecules). This suggests that the second law is essentially a statistical one. It is theoretically possible to toss 100 coins and have them all coming out heads, but the probability of this happening is extremely low. In terms of probability, the second law claims that entropy always increases. More precisely, it states that this is the most probable outcome of any physical change. It is theoretically possible for entropy to spontaneously decrease, but for any system with a large number of entities, it is highly improbable.
| Macrostate | Number of microstates (note many rows have been omitted) |
|
|
Heads |
Tails |
Ω |
|
100 |
0 |
1 |
|
99 |
1 |
1.0 x 102 |
|
90 |
10 |
1.7 x 1013 |
|
80 |
20 |
5.4 x 1020 |
|
60 |
40 |
1.4 x 1028 |
|
55 |
45 |
6.1 x 1028 |
|
50 |
50 |
1.0 x 1029 |
|
45 |
55 |
6.1 x 1028 |
|
40 |
60 |
1.4 x 1028 |
|
20 |
80 |
5.4 x 1020 |
|
10 |
90 |
1.7 x 1013 |
|
1 |
99 |
1.0 x 102 |
|
100 |
0 |
1 |
Pierre-Simon, marquis de LaPlace (b1749 - d1827) in the nineteenth century proposed a form of scientific determinism. Briefly stated, he surmised that a sufficiently advanced science would be able to determine the exact velocity and position of all of the particles in the universe. Using this information a person, in theory could predict all future events. Werner Heisenberg's (b1901 – d1976) uncertainty theory made this form of determinism impossible. Quantum determinism is similar in that it can predict the future behavior of quantized matter. Extrapolating this to a super advanced civilization, it is once again possible to predict the future mathematically.
Information is deemed by some to be a measure of entropy. A single letter or bit of binary carries very little information and as such has very low entropy. As more information is contained within a body (such as mass, velocity, quantum wave functions etc.), the entropy contained within that body also increases. Complex systems contain a great deal of information and as such have large amounts of entropy. Some physicists look at all matter and energy as merely information carried by the wave functions of the constituent parts of the body.
Black holes are locations in which the gravitation of a collapsed star is so great it warps space to the point where it creates a singularity of infinite density. The black hole has only mass, charge, angular momentum and entropy. All of the complexity and attendant information (entropy) contained in the uncollapsed star is reduced to the above simple properties. According to Stephen Hawking (b1942 -) and Jacob D. Bekenstein (b1947 -), the entropy of the black hole only determines the area of the event horizon, nothing else. This is the no hair theorem proposed by Roger Penrose (b1931 -). Where has all of the information originally contained within the star gone? Has the second law of thermodynamics been violated in that entropy is lost forever, causing the entropy of the universe to decrease?
Hawking has proposed that black holes aren’t so black - as they radiate energy at the event horizon due to quantum fluctuations. Does this radiation contain the information carried by the collapsing star and anything else, which has fallen into the black hole? If the information is only thermal then the answer is no. The Hawking radiation caused the black hole to eventually “evaporate” (over an unbelievably long period of time). If the Hawking radiation does not carry the information it is lost forever and the second law is violated.
Suppose you tossed a book into a black hole? The book would be lost forever and add to the area of the event horizon, however the information contained within the book is irretrievable. This presents a big problem to those who believe the second law of thermodynamics is inviolate. It's certainly possible that the entropy of matter falling into a black hole can be traced as the matter crosses the horizon; opinions on this differ. But, first of all, you are not going to get enough entropy to account for the (enormous!) Bekenstein-Hawking entropy of the black hole -- a very high entropy black hole can be formed from very low entropy matter. If you want to account for black hole entropy this way, there's a sense that you can, but to do that you have to count up all of the different possible ways the black hole could have formed, not just the particular way it did. The information loss paradox is a quantum mechanical one: you can, it seems, form a black hole from a pure quantum state, and then have it evaporate by Hawking radiation into a mixed state. Such a transition from a pure state to a mixed state violates the standard rules of quantum mechanics. It's called ``information loss'' because, basically, you lose information about the quantum state of the universe.
The concept of complexity is more difficult to pin down. A physical system that we consider to be 'complex' represents a delicate compromise between mindless simplicity and pure randomness. This idea can best be illustrated graphically. In the left box, the points are arranged in a regularly spaced grid (like a crystal). This simple arrangement carries with it little information and can be described by a single number specifying grid spacing. If new points were to be added, one knows exactly where to put them.

The opposite extreme is the middle pattern, which depicts a random collection of points. This arrangement of points requires a great deal of information to describe. Because the location of each point is random and unrelated to any other, the x and y coordinates of each and every point must be specified to define the pattern. Such a random pattern carries the maximum amount of information. If a point is to be added to the pattern, one has no idea where the point should be placed.
The pattern on the right illustrates a more interesting pattern, one that is simultaneously more structured than random points and encodes more information than the simple grid at the top. If a new point is to be added one would have some idea where it might fall, and yet it is not completely specified in advance as in the simple grid. Complex and interesting patterns negotiate the proper compromise between simplicity and randomness.
* By physicist Fred Adams, with the help of illustrator Ian Schoenherr, Our Living Multiverse 2004, Pi Press (New York) and Origins of Existence 2006
![]()
to next experiment
to e-Physics menu
to site menu