an enormously important topic
with 5 experiments
![]()
![]()
Our human ancestors left evidence nearly 800,000 years ago of their early use of fire. Likely that skill was accompanied by early concepts of what we now call heat. Our earliest knowledge of that conception of heat came much later. Heracleitos of Ephesos (Greek, flourishing 484 B.C., who remarked: Much learning does not teach understanding,
) wrote that despite appearances, there must be some unity of substance in the universe and proposed it was fire. That was consistent with his second principle that everything is in eternal flux. A third principle noted that the apparent disharmony in the world hides a profound harmony. His ideas were eventually merged into the theory by Empedocles of Agrigentum (492 to about 400 B.C.) that everything is composed of combinations of four elements: Earth, Water, Air, and Fire. Aristotle of Stageira (384 to 322 B.C.) incorporated that into his compilation of all knowledge which was taught in many parts of the world for the next 2000 years.
Alchemy began as an Arab mixture of Egyptian arts of dyeing, painting, glass making, pyrotechnics, medical drugs, mining, and metallurgy with the theories of the Greeks (mostly Aristotle's) to explain changes in color and appearance of materials. One of the main goals of alchemists was to learn the proper proportions of ingredients and processes to cause one element to undergo transmutation to another element (such as making Copper into Gold). The earliest known Alchemists were Zosimus and Synesius (perhaps of the 3rd Century A.D.). Writings attributed to them described practical laboratory operations, but used obscure symbols, probably to maintain Alchemy secrets. Over 200 alchemy books are attributed to Jabir ibn Hayyan (722 to 815 A.D.). He place emphasis on first hand knowledge of materials: For he who performs not practical work nor makes experiments will never attain to the least degree of mastery. ...Do thou experiment so that thou mayest acquire knowledge.
The application of heat by fire was one of their primary tools. Abu Bakr Muhammad ibn Zakariya al-Razi, a Muslim called Rhazes (860 to 925 A.D.) was the first of a series of physicians that were the chief contributors to chemistry for the next 500 years. Abu 'Ali al Husain ibn Abdallah ibn Sena called Avicenna in Europe (b980, d1037) was the greatest physician of Islam. His Canon
of medicine became the standard reference for the next six centuries. One of the last of the alchemists, Joseph Black of Edinburgh (b1728, d1799) suggested that Chemistry is but the study of heat.
Chemistry was radically changed by the 1789 publication of Traite elementaire de Chimie...
by Antoine Lavoisier (Paris, b1743, d1794). He carefully documented the benefit of replacing the four element theory of the alchemists with a new definition of element based on what cannot be separated into distinct materials. To encourage adoption of his new ideas, he realized the importance of also changing vocabulary and nomenclature. What to the alchemists was fire, Lavoisier now divided into Lumiere (light) and Calorique (calories = heat). With discoveries now being achieved as hobbies of the wealthy, the earlier need to maintain secrecy in order to provide a living were replaced by a willingness to publish and share ideas. Lavoisier's ideas spread rapidly bringing a flourish of further discoveries.
It is customary to think of our concepts as facilitating and guiding our lives, fostering the progress we achieve. But here is an example of how that guidance also restricts our creative ideas to those which match our current understanding. Starting with the Greeks mentioned above, the accepted view was that fire with its heat and light are substance like all the materials of our universe. The alchemists had established that the way to measure substances is by weight, (or alternatively volume). But both light and heat seemed to have no measurable weight or volume. It wasn't until a physicist tried to improve the boring of cannon barrels did anyone gather convincing evidence that heat isn't a material substance.
 Benjamin Thompson (b1753 in Woburn, Massachusetts, d1814, portrait at right→), scallywag, Tory spy in the American colonies, and later nobility as Count Rumford, was given the authority to make radical improvements in the Bavarian army. To accomplish that, he conducted experiments which led him to write:
Benjamin Thompson (b1753 in Woburn, Massachusetts, d1814, portrait at right→), scallywag, Tory spy in the American colonies, and later nobility as Count Rumford, was given the authority to make radical improvements in the Bavarian army. To accomplish that, he conducted experiments which led him to write:
Being engaged, lately, in superintending the boring of cannon, in the workshops of the military arsenal at Munich, I was struck with the very considerable degree of Heat which a brass gun acquires in a short time, in being bored; and with the still more intense Heat (much greater than that of boiling water, as I found by experiment) of the metallic chips separated from it by the borer. (Early on he found the chips removed by drilling still had precisely the same heat capacity as the original metal!)So Count Rumford effectively removed both Lumiere and Calorique from Lavoisier's list of chemical elements. Neither light nor heat are substances.The more I mediated on these phenomena, the more they appeared to me to bid fair to give a farther insight into the hidden nature of Heat; and to enable us to form some reasonable conjectures respecting the existence, or non-existence, of an igneous fluid; a subject on which the opinions of philosophers have, in all ages, been much divided.
It is hardly necessary to add that anything which any insulated body, or system of bodies, can continue to furnish without limitation, cannot possibly be a material substance; and it appears to me to be extremely difficult, if not quite impossible, to form any distinct idea of anything capable of being excited and communicated in these Experiments, except it be Motion.
It might be remembered here that chemistry and physics developed as two very distinct human endeavors. Alchemy was a craft of how to change material substances protected by secret symbols and rituals. Physics was an esoteric pondering of the forces of the universe, particularly the motions of the heavens. Many in each field had considerable distain for anyone who practiced the other. Very few people dabbled in both. (So the field of Physical Chemistry didn't much occur until Josiah Willard Gibbs published a paper in 1876 applying several concepts from physics to chemistry.)
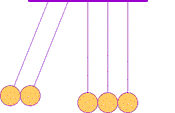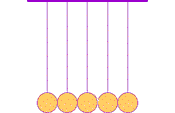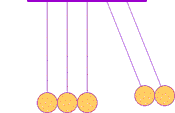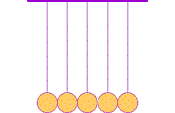 The first clear ideas about energy were developed to understand the common behavior of moving objects:
The first clear ideas about energy were developed to understand the common behavior of moving objects:
With the concepts of work and kinetic energy established, it follows that an object rising against the force of gravity will have work done on it causing it to slow. While falling the gravity will continue to do work, restoring the lost speed. It is convenient to think of the rising object as moving the kinetic energy into potential energy stored in the gravitational field. The energy comes out of storage and returns to motion as the object falls. That allows us to observe that the total of kinetic energy and potential energy is conserved in projectile motion.
So when energy was first clearly defined, there were only kinetic and potential energy. The interesting property of nature is that is allows for this simple, useful and easy to use scheme for helping us understand motions. The amazing and delightful thing is that the scheme could be expanded by adding other forms of energy and other forces to make a great universal conservation scheme, a very powerful part of science. It is summarized the the First Law of Thermodynamics which states that energy is ALWAYS conserved.
One of the early uses of this scheme was to understand steam and internal combustion engines where work is done to compress a gas,Two and a half centuries ago the calorie was developed as part of an empirical system (not based on theory) for measuring heat based on the assumption that heat was a conserved substance. The procedure to measure heat was to simply allow the heat to warm water, then multiply the temperature rise of the water (in °C) by the mass of water (in grams). But it was a century later that heat was added as a form of energy, rather than a form of matter.
But not all substances heat as readily as water. To adjust for the heat capacity of another substance, the calculation of that substance's heat requires multiplication by a correction factor called the substance's specific heat. Must substances have a specific heat less than one, meaning that they heat easier than water. The rather large heat capacity of water results in oceans and other large bodies of water having a moderating effect on the Earth's weather.

 There is potential energy stored in the electrical fields associated with chemical bonds inside molecules. That stored chemical energy is referred to by the term enthalpy (from the Greek ενθαλπος = enthalpos, meaning to put heat into; its symbol = H). Usually enthalpy is not determined directly, but a change in enthalpy can be measured by promoting a chemical reaction in an insulated apparatus (called a calorimeter) so that the temperature of surrounding water changes. Josiah Willard Gibbs (b1839, d1903, photo at right→) of Yale U, introduced a heat function for constant pressure in 1875. The Dutch physicist Kamerlingh Onnes (← photo at left, b1853, d1926, winner 1913 Nobel Prize in Physics) in the first years of the 20th century introduced the relationship
There is potential energy stored in the electrical fields associated with chemical bonds inside molecules. That stored chemical energy is referred to by the term enthalpy (from the Greek ενθαλπος = enthalpos, meaning to put heat into; its symbol = H). Usually enthalpy is not determined directly, but a change in enthalpy can be measured by promoting a chemical reaction in an insulated apparatus (called a calorimeter) so that the temperature of surrounding water changes. Josiah Willard Gibbs (b1839, d1903, photo at right→) of Yale U, introduced a heat function for constant pressure in 1875. The Dutch physicist Kamerlingh Onnes (← photo at left, b1853, d1926, winner 1913 Nobel Prize in Physics) in the first years of the 20th century introduced the relationship
When doing an experiment to calculate the change in enthalpy, we can often maintain a constant pressure so that the term Δ ( p V ) = 0, simplifying the equation. But it is crucial to remember that what we actually measure is the change in temperature of the surrounding water. So we start by calculating the change in energy of the environment
and then note that to conserve energy the chemicals of interest must have had the opposite change. That is, if the water WARMED, the reaction was exothermic (exo = out of) and the chemicals in the reaction LOST energy: ΔH will be NEGATIVE. If the surrounding water COOLED, the reaction was endothermic (endo = into) and the chemicals GAINED energy: ΔH will be POSITIVE.
Now everyone has noticed since infancy that balls spontaneously roll downhill but never uphill. There seems to be a tendency in the universe for stored potential energy to decrease whenever possible. A new chemist might extrapolate to believe that the same holds true with energy stored in chemical bonds. When possible chemical reactions would spontaneously release energy. That would suggest that all spontaneous chemical reactions should be exothermic. But some reactions (like ice melting in a warm room) are endothermic. If we don't want to abandon our hunch that the universe tends to decrease stored energy, there must be some other competing factor which sometimes prevails. That second factor in determining what changes happen in our universe is entropy. Entropy (symbol S) represents the potential for disorder
in a system. The universe also has a tendency to be more disordered. (When ice melts, the water molecules are more disorganized than when they maintained specified positions in the solid ice lattice.) The second law of thermodynamics states that the entropy of an isolated system (one lacking outside influence) can only remain constant or spontaneously increase.
If ΔH is positive, the reaction is endothermic, that is heat is absorbed by the system due to the products of the reaction having more enthalpy than the reactants. If ΔH is negative, the reaction is exothermic with the overall decrease in enthalpy achieved by the release of heat to the surroundings.
This experiment is a bit more vague that P10.1 because the solutes needed will depend on what you can obtain locally and what you feel comfortable and competent to safely use. (In the formation of a uniformly mixed solution, the material, usually a liquid, in greater abundance is called the solvent, and the materials, often a solid, in lesser abundance is called the solute.) Many materials will dissolve in water. It would be preferable to find at least one which generates heat when dissolved and another which cools the water. Sodium hydroxide (ancient name lye), NaOH is a solid, corrosive to skin, eyes and clothing, but often available for sale as a drain cleaner. It is noticeably exothermic. If you choose to use NaOH, you should wear protective clothing such as a rubber or plastic apron, non-porous gloves, and especially protective eye goggles. For spills on skin or clothing, DON'T PANIC, but immediately wash with water until it no longer feels slippery.
For eye contact (which sometimes stings!), DON'T PANIC, but immediately flush with comfortable temperature water (even though it tickles) for at least 15 minutes then get immediate medical attention. Even a tiny splash in an eye can cause delayed blindness so take this seriously. Other substances may be nearly as dangerous. READ the LABELS and follow all recommended precautions. Other granular solids such as sugar and table salt (NaCl) may be much safer but may require measurement of tiny temperature changes. Pure liquids such as ethanol and acetone might also be used, giving appropriate caution to those which are flammable.
The extent a substance dissolves in water is influenced by the disassociation by many ionic substances into electrically charged ions in water. Each ion is surrounded by an entourage of polar (lopsided electrically) water molecules. The somewhat negatively charged Oxygen in the water are attracted to positive ions while the somewhat positively charged Hydrogen in the water are attracted to the negative ions. How much more disordered the ions are in this arrangement compared to their original crystal lattice and the strength of bonding in both situations varies from substance to substance. The result is that some substances dissolve exothermically, others endothermically, while still others there is little energy change.
environmental watergained, determine the amount of heat the
newly formed watermust have lost in the formation of the new bonds.
new waterwas formed, multiple the measured heat by 10 to calculate the Molar heat of Neutralization.
Compare of the Heats of Fusion, Solution, and Reaction. The differences in the magnitudes of their values gives a rough measure of the different strength of the chemical bonds changing (as was discussed earlier in Investigation P5: Condensed Matter & Transitions.)
Food is the fuel for man and beast; it provides chemical energy which is carried by the blood stream to muscles and other organs which need energy to function. The chief food substances — starch, sugas, fats and proteins — are large molecules built up of smaller molecules linked together. The linking and unlinking of the small molecules, such as in animal digestion, are relatively simple reactions catalyzed by enzymes but not involving much transfer of energy.
Energy is mainly obtained from food in each individual cell by an elaborate series of steps. For example the common sugar glucose, C6H12O6, is in a multistep process broken in half, then six molecules of water are stripped off, and finally the Carbon atoms are joined with Oxygen from the lungs to make six molecules of CO2. By using a large number of nearly reversible steps, a maximum amount of energy is captured in other molecules such as ATP which transport it to processes which require energy to occur. Still, an appreciable amount of heat is released which keeps us living creatures warmer than our environments.
Because energy is conserved, the amount of energy released by a chemical reaction, such as glucose burning to carbon dioxide and waterBut be cautioned, our culture often plays interesting tricks on us. The food industry is required by government to specify the energy values on food labels in calories. But because the number of calories is often moderately large, the unit specified is actually kilocalories, but strangely labelled as (note capital C) Calories, i.e., big Calories as opposed to our normal little calories.
Finding entropy directly pretty much requires determining all the equal possibly arrangements for a system. For a system involving a ponderable amount of chemical substances with a mole or more of molecules, that task in unreasonably large. So it is common to settle for the comparatively trivial task of calculating the the change in entropy of a selected process in a specified system. The trick is to recall that the Gibbs Free Energy represents the tendency for a reaction to occur (if its value is negative) or for the reverse to occur (if the value is positive). And when a system has reached equilibrium there is no tendency for the reaction to go either way: Δ G = 0 !
![]()
to next experiment: Sound
to menu for Nanochemistry, Colloidal & Physical Chemistry
to ie-Chemistry menu
to site menu