arrangement of atoms in solids
Atoms in solids generally occupy set positions. Those positions and their chemical bonds maintaining those positions determine almost all the important physical properties of solids. So there is value in studying the most common of these lattice arrangements.
First, we should recall that some solids which we call glass, are amorphous, meaning without form. When broken these solids typically fracture forming curved surfaces. They generally lack precise melting temperature, gradually softening over a temperature range suggesting that the strength of forces between atoms varies considerably as distances between atoms varies due to irregular packing arrangements. For the present we will turn attention to those solids which have a repeating structural pattern, called crystalline. These generally have precise and characteristic melting temperatures, and if brittle, cleave such that the new flat surfaces which form indicating their lattice layering.
We should note that metals also use lattice arrangements. But these typically shiny, often silver colored solids which are good conductors of heat and electricity, allow slippage between their layers such that they are malleable and ductile, deforming rather than cleaving under stress. We shall find that all these properties can be understood and predicted in terms of their lattice.
Obviously real atoms are too small to see their lattice arrangement. Yet crystals containing enormous numbers of atoms, when grown free from hinderance, exhibit a shape characteristic of the lattice. Since early 20th Century, it has been possible to confirm lattice of crystals by X-ray diffraction and more recent techniques such as scanning tunneling microscopy.
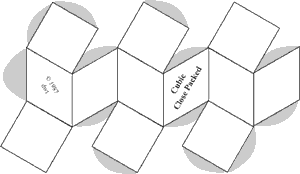
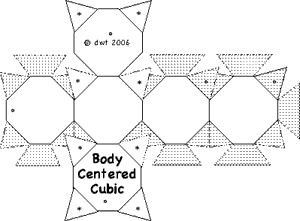
It is often valuable to create models to help understand the behavior of complicated systems such as collections containing large numbers of atoms and molecules. Sometimes those models are mathematical. But visual models, either virtual on computers, or physical models, can improve understanding. Of course models are never exactly like the things being modeled. But value occurs when the model shares and illustrates many features with the real thing. In this experiment paper templates can be folded to represent atoms which join together in patterns characteristic of four common lattice.
Print several pages of each paper template by either clicking each image to obtain full page gif images or by opening PDF files for lattices called
Construct a minimum of atoms to make each unit cell described in the table below. (8 additional Cubic Close Packed atoms will be needed if you wish to construct Face Centered Cubic lattice.
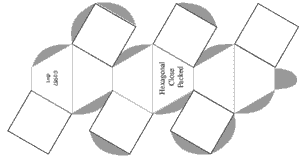
| Lattice | Unit Cell layering | Glide difficult |
Coordination number |
Features | Examples |
| Simple Cubic | 4 + 4 = 8 | ||||
| Hexagonal Close Packed | 3 + 7 + 3 = 13 | ||||
| Cubic Close Packed | 3 + 7 + 3 = 13 | ||||
| Body Centered Cubic | 4 + 1 + 4 = 9 | ||||
| Face Centered Cubic | 1 + 6 + 6 + 1 = 14 |
peaksof atoms. Why aren't the other three used? Now also place the remaining appropriate small layers on top of the large layers. Note whether the top atoms occupy the same positions as the bottom layer, or the alternate positions. Do the position of atoms alternate every other layer, or every third layer? (...finally differences between the two kinds of lattice!)
You might reflect on the difficulty envisioning the three dimensional geometry. This may be a skill area than many people haven't well developed?
Communicating technical information such as observations and findings is a skill used by scientists but useful for most others. If you need course credit, use your observations in your journal to construct a formal report.
Recall that there is an energy advantage (universal preference for minimum stored energy; e.g., balls roll down hill!) for atoms to have fully occupied electron energy levels (or equivalently, empty energy levels). So chemicals react so their atoms with partially filled energy levels either empty or fill those levels. In some cases this is achieved by taking or giving electrons (resulting in ionic bonding), but other substances share electrons to fill energy levels (resulting in covalent bonding).
The substances, classified as metals since long before electrons were known, occupy the left side of typical periodic charts, indicating they have few valence electrons. Having few valence electrons, metals often relinquish those valence electrons to non-metals, forming ionic salts. Since metals have less than four valence electrons, in the absence of nonmetals pure metals cannot reach minimum stored energy by either traditional covalent bonding or ionic bonding. Metals solve that apparent dilemma by using a variation of covalent bonding. Instead of sharing pairs of electrons between two atoms, valence electrons are communally shared with all neighboring metal atoms.
These light mass, mobile electrons can also carry kinetic energy faster than heavier atoms help solidly in their lattice positions. So the communal electrons are responsible for metals conducting heat better than other materials. That is why we use metal cookware when we are interesting in fast cooking, and non-metal cookware where cooking delicate food that easily scorches.
Ionic Solids are the result of a non-metal with high electronegativity essentially pulling one or more electrons away from a metal with low electronegativity resulting in ions with opposite electrical charges. Since opposite electrical charges attract, the ions pack together in lattices that allow opposite charged ions to be closer together than identically charged ions. If you consider arranging ions in either of the close packed lattices, you will find it impossible to do so without having adjoining identical ions. Thus ionic solids seem to prefer the less compact forms of lattice rather than a close packed lattice. Can you guess the type of lattice in the NaCl (table salt) shown at right?
If you are not familiar with cleavage, you might view a short video of a NaCl crystal being cleaved.
For covalently bonded materials, the shape of the particular molecule is most important. (The non-metals on the chart are white because at room conditions they form molecules rather than pack in lattice.) Typically the bonds within each molecule are strong while bonds between molecules are much weaker. So if the molecules are relatively small, the substances are often gases or liquid at room temperature. But larger molecules and network solids (held together by a network of covalent bonds) may use lattice structures. And smaller molecules form solids at higher pressures or lower temperatures. Can you guess the kind of lattice in the SiO2 (quartz) shown at right?
to Inorganic Chemistry menu
to e-Chemistry menu
to site menu
