Physical Science
Problems 4
Understanding the Past & Present, Predicting the Future
Scientists try to understand the world. Scientists determine if their understanding is valid by making PREDICTIONS then checking if those predictions are correct. Precise mathematical quantities are considered better predictions than vague word descriptions. Science can't actually PROVE their understanding is TRUE. The best scientists can do is to check predictions. So solving problems and making predictions are essential to establish the VALIDITY of the scientific theories. This checking against reality is the part of science that distinguishes it from philosophy. Beyond just being a part of science, checking the predictions is the very aspect of science that makes science so valuable to civilization. Without solving problems (i.e., making and checking predictions) you really haven't learned the skills of science.
The following problems are intended to focus your thinking, help you understand our world, and to make predictions that are verifiable. Keep your thoughts and predictions for these problems in your journal. Include sufficient information so you can later refer back to your journal to refresh your thoughts and memories.
- If 0.50g of solid is the maximum soluble in 5.0 cm3 of water, calculate the concentration of the solution in units of g/cm3 and g/100 cm3. This latter is the preferred way to communicate information about solubilities.
- A mass of 25.0 g of sugar is dissolved in 150 cm3 of water. What is the concentration in
- g/cm3?
- g/10 cm3?
- g/100 cm3?
- Each of four capped containers contains 10 cm3 of water at 25°C. Masses of an unknown powder are placed in the containers as follows: 4 g, 8 g, 12 g, 16 g. All the capped containers are shaken for several minutes. All of the powder dissolved in the first two containers but powder remains in the last two containers.
- Why is there still powder left in the last two containers?
- What is the solution's concentration in each of the first two containers?
- What can you say about the concentration of the solutions in the last two containers?
- The following information is obtained from several sources for solubilities at 0°C. For each one calculate the solubility in the standard format of g/100 cm3 of water.
| Boric acid |
0.20 g in 10 cm3 of water |
| Bromine |
25 g in 600 cm3 of water |
| Washing soda |
220 g in 1000 cm3 of water |
| Baking soda |
24 g in 350 cm3 of water |
- From the above table, determine how much material would be needed to make a Liter of saturated solution for each.
- In many localities, after a kettle has been used for some time for boiling water, a flaky solid appears on the insides of the kettle that have been in contact with the water. How do you account for the presence of this
boiler scale?
- Suppose that 200 cm3 of a saturated solution of the solid, potassium nitrate, were left standing in an open container for three weeks. During this time most of the water evaporated.
- Would the mass of potassium nitrate dissolved in the solution change?
- Would the concentration of potassium nitrate in solution change during the three weeks?
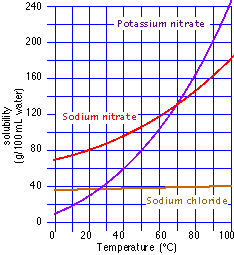
- Consider information from the graph at right. If you had a saturated solution of potassium sulfate at room temperature, what would you predict will happen if you
- heat the solution?
- cool the solution?
- What temperature would be required to dissolve 110 g of sodium nitrate in 100 cm3 of water?
- If 20 g of sodium chloride is dissolved in 100 cm3 of water at 20°C, it the solution saturated?
- How could you experimentally test if a solution is saturated?
- How can you use a solubility to chart to determine in a known concentration of solution is saturated?
- A mass of 30 g of potassium nitrate is dissolved in 100 cm3 of water at 20°C. The solution is heated to 100°. How many more grams of potassium nitrate must be added to saturate the solution?
- A mass of 10 g of sodium nitrate is dissolved in 10 cm3 of water at 80°C. The solution is cooled. At what temperature will a precipitate first appear?
- Properties for three unknown substances, labeled X, Y, and Z, have been determined and shown in the table below. Which, if any, of the substances could be the same?
| Substance |
Density
(g/cm3) |
Melting point
(°C) |
Boiling point
(°C) |
Solubility in water
at 20°C
(g/100 cm3)
|
Solubility in methanol
at 20°C
(g/100 cm3) |
| X |
1.63 |
80 |
327 |
20 |
insoluble |
| Y |
1.63 |
81 |
326 |
19 |
insoluble |
| Z |
1.62 |
60 |
310 |
156 |
insoluble |
- Carbonated beverages are saturated solutions of carbon dioxide with additional dissolved solutes to provide taste and flavor.
- When a carbonated beverage is first opened there is the sound of escaping gas, bubbles form in the liquid and foam forms on the top. What is happening to the concentration of dissolved gas? Why was the concentration different before the container opened?
- When a carbonated beverage is allowed to remain in an open container it becomes
flat.
Use what you know about acids to explain the connection between the carbon dioxide gas and the loss of tangy flavor.
- Warm carbonated beverages go flat faster while even open carbonated beverages stored in a refrigerator will remain tangy for many hours. What do these observations say about how the solubility of gases such as carbon dioxide depends on temperature?
- Limewater is a saturated solution of the white powder called lime, Ca(OH)2 which sometimes is used to make the white lines on sports fields. A limewater solution keeps poorly because carbon dioxide present in small concentrations in air gradually reacts with the lime making chalk, CaCO3. Traditionally limewater has been used as an easy test to identify carbon dioxide. A gas is likely carbon dioxide if when it is bubbled through limewater a cloudiness formed by chalk occurs. If 4.2 g of baking soda, NaHCO3, is placed in 100.0 g of vinegar, a gas will form leaving behind a solution of mass 102.0 g. At one atmosphere pressure about 1200 mL of a gas can be connected which reacts to turn limewater cloudy. Identify the gas and determine its density.
- Water analysis usually give concentrations of dissolved substances in parts per million (ppm). If the concentration of table salt, sodium chloride (NaCl), in drinking water is 14 ppm, what would its concentration be in g/100 cm3? (Human tastes buds don't detect concentrations of NaCl below about 25 ppm so this water wouldn't taste salty.)
- If you need to dissolve a solid in water you can often hasten dissolving. How would each of the following procedures make solid dissolve faster?
- Stirring or shaking the water.
- Crushing the solid into smaller pieces.
- Heating the water.
![]()
![]()

![]()